Copilotでブロンプトを書いてさまざまなプログラミング言語のコードを作成することができます。例えば、Rのスクリプトを作成できます。
一つの例として、RのTrialSizeというサンプルサイズを計算するためのパッケージを使って、Time-to-event (時間イベント分析)(生存分析)で2群のハザード率を比較するのに必要なサンプルサイズを計算するスクリプトの作成を試みてみました。
TrialSizeの関数の内、TwoSampleSurvival.Equalityが差があるかどうかを分析するために必要なサンプルサイズを計算する関数です。この関数は8つの引数を設定します。TrialSizeのマニュアルの該当箇所に以下の様に書かれています。
TwoSampleSurvival.Equality(alpha,beta,lam1,lam2,k,ttotal,taccrual,gamma)
この関数の演算結果を変数resに格納するというスクリプトは以下の様になります。ここまでは自分で考えて書きます。
res=TwoSampleSurvival.Equality(alpha,beta,lam1,lam2,k,ttotal,taccrual,gamma)
そこで、Copilotに次のように聞いてみました。
RのパッケージTrialSizeの関数res=TwoSampleSurvival.Equality(alpha,beta,lam1,lam2,k,ttotal,taccrual,gamma)について解説してください。lam2が対照群、lam1が介入群のハザード率とします。
その回答は以下の通りです:
TwoSampleSurvival.Equality は、Rの TrialSize パッケージに含まれる関数で、生存データの指数モデルにおける2群のハザード率の差を検定するために使用されます。
関数の概要
この関数は、介入群(lam1)と対照群(lam2)のハザード率が等しいかどうかを検定するために設計されています。帰無仮説(H0)と対立仮説(Ha)は以下のようになります:
- H0(帰無仮説): 介入群と対照群のハザード率の差はゼロである(等しい)
- Ha(対立仮説): 介入群と対照群のハザード率の差はゼロではない(異なる)
引数の説明
この関数には以下の引数があります:
alpha:有意水準(例:0.05)beta:検出力(power = 1 – beta)lam1:介入群のハザード率lam2:対照群のハザード率k:サンプルサイズ比(k = n1/n2)ttotal:試験の総期間taccrual:被験者登録期間gamma:指数分布のパラメータ(gamma = 0の場合は一様な患者登録を仮定)
使用例
以下のコードは、TwoSampleSurvival.Equality を使用した例です:
Example.7.2.4 <- TwoSampleSurvival.Equality(0.05, 0.2, 1, 2, 1, 3, 1, 0.00001)
print(Example.7.2.4)
このコードでは、有意水準 0.05、検出力 0.2、介入群のハザード率 1、対照群のハザード率 2 などのパラメータを設定し、検定を実行しています。
この関数を使うことで、介入群と対照群の生存率に統計的な有意差があるかどうかを評価できます。試験デザインの計画やサンプルサイズの決定に役立つでしょう。
試してみて、何か疑問があれば教えてください!📊###ここまでCopilotの回答。
さて、実際に動かせるスクリプト例が出力されているので、Rを起動して、ファイルメニューから新しいスクリプトを開いて、library(TrialSize)と書き込んで、それに続けて、スクリプトの部分をコピーして、ペーストします。そして、Rのエディタウインドウで全体を選択して、実行ボタンをクリックして実行します。

結果がコンソールに出力されますが、TwoSampleSurvial.Equality関数を実行した次の行に2つの数値が出力されていますが、まずこれが何かについてCopilotに聞いてみましょう。
実行すると2つの値がコンソールに出力されますが、これは何でしょうか?
Copilotの答えは、介入群(n1)のサンプルサイズと対照群(n2)のサンプルサイズですということでしたが、これは明らかに間違っています。そこで、TwoSampleSurvival.Equalityの関数のスクリプトを提示してもらい、関数の中身を確認しよう思います。
TwoSamplSurvival.Equality関数のスクリプトを見せてください。
得られた回答は、RDocumentationやQuantargoやrdrr.ioを参照しろというものでした。そこで、この関数のスクリプトをRで表示させる方法がないか聞いてみました。
TrialSizeにこの関数のスクリプトを提示するようにするRの関数はありますか?
次の回答が得られました:
Rには、関数のソースコードを表示するための関数 がいくつかあります。TrialSize パッケージの TwoSampleSurvival.Equality 関数のスクリプトを確認するには、以下の方法を試してみてください。
1. getAnywhere() を使用
getAnywhere() 関数を使うと、パッケージ内の関数のソースコードを表示できます:
getAnywhere(TwoSampleSurvival.Equality)
この方法は、関数がエクスポートされていない場合でもコードを確認できることがあります。
2. TrialSize パッケージをロードして print()
関数がオブジェクトとして格納されている場合、print() を使うことでコードの一部を確認できることがあります:
library(TrialSize)
print(TwoSampleSurvival.Equality)
ただし、関数がコンパイル済みである場合は、ソースコードが表示されないことがあります。
3. body() を使用
関数の本体部分を取得するには、body() を使います:
body(TwoSampleSurvival.Equality)
これにより、関数の処理内容を確認できます。
4. deparse() を使用
関数のコードを文字列として取得するには、deparse() を使います:
deparse(TwoSampleSurvival.Equality)
この方法では、関数のコードがリスト形式で出力されます。
関数のソースコードが非公開の場合、これらの方法では表示できないこともあります。その場合は、パッケージの公式ドキュメント や GitHubリポジトリ を確認するのが良いでしょう。
試してみて、うまくいかなかったら教えてください!📊###ここまでCopilotの回答
Copilotの回答の中から、getAnywhere(TwoSampleSurvival.Equality)でこの関数の情報が得られそうだとわかったので、これをRで実行したところ、この関数の中身がコンソールに出力されました。
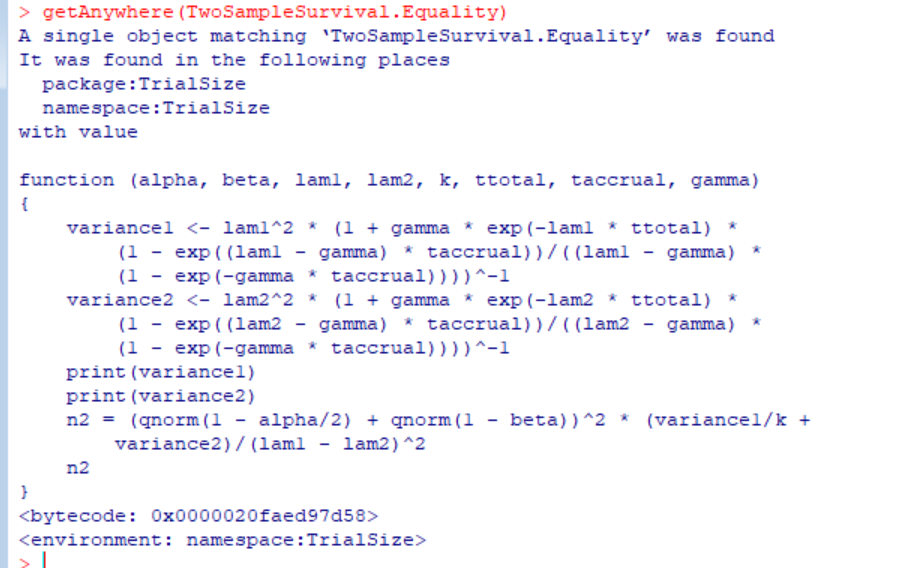
このスクリプトを見ると、print(variance1)とprint(variance2)というコードがあるので、上記の2つの値は、lam1すなわち、介入群のハザード率の分散とlam2すなわち対照群の分散の値だということが分かりました。(各分散の計算式は、TrialSizeの作者らの著書”Chow SC, Shao J, Wang H, Lokhnygina Y: Sample Size Calculations In Clinical Research. CRC Press, Taylor & Francis Group, 2018, New York, NY, USA.”の150ページに書かれているものと同じでした。TrialSizeの作者の著書なので。)
そして、この関数はn2を返す関数なので、結果には対照群のサンプルサイズが格納されていることになります。そして、上記の引数の解説からわかるように、介入群のサンプルサイズはその値にkを掛け算して得られるはずです。
ここで、スクリプトを、より一般的な目的に合わせて書き換えようと思います。引数の値をあらかじめ上記の例と同じ値に設定し、TwoSampleSurvival.Equality関数を実行します。結果は変数resに格納されます。以下の様にCopilotに指示しました。
Example.7.2.4 <- TwoSampleSurvival.Equality(0.05, 0.2, 1, 2, 1, 3, 1, 0.00001) print(Example.7.2.4) このスクリプト書き換えて、各引数を同じ名前の変数にこの例と同じ値を設定し、結果は変数resに格納するスクリプトを書いてください。最初にライブラリの読み込みのスクリプトも追加してください。結果は、対照群のサンプルサイズ、介入群のサンプルサイズ、総サンプルサイズを出力するようにしてください。なお、resには対照群のサンプルサイズが格納されます。
その回答は:
以下のRスクリプトでは、TrialSize パッケージを読み込み、各引数を同じ名前の変数に設定した上で、TwoSampleSurvival.Equality() を実行し、結果を res に格納します。res には対照群のサンプルサイズが格納されるため、そこから介入群のサンプルサイズと総サンプルサイズを計算し、出力するようにしています。
# ライブラリの読み込み
library(TrialSize)
# 各引数の設定
alpha <- 0.05
beta <- 0.2
lam1 <- 1 # 介入群のハザード率
lam2 <- 2 # 対照群のハザード率
k <- 1 # サンプルサイズ比 (n1/n2)
ttotal <- 3
taccrual <- 1
gamma <- 0.00001
# サンプルサイズの計算 (対照群のサンプルサイズ)
res <- TwoSampleSurvival.Equality(alpha, beta, lam1, lam2, k, ttotal, taccrual, gamma)
# 介入群のサンプルサイズを計算
n1 <- k * res # 介入群のサンプルサイズ
n_total <- n1 + res # 総サンプルサイズ
# 結果の出力
cat("対照群のサンプルサイズ:", round(res), "\n")
cat("介入群のサンプルサイズ:", round(n1), "\n")
cat("総サンプルサイズ:", round(n_total), "\n")
このスクリプトを実行すると、res に対照群のサンプルサイズが格納され、そこから介入群と総サンプルサイズを計算して出力します。round() を使って整数値に丸めていますが、必要に応じて調整してください! 📝✨###ここまでCopilotの回答。
見たところ、結果の出力のスクリプトの部分は少し問題がありそうですが、まずそのままスクリプトをコピーしてRで実行させてみます。エラーが起きることなく、サンプルサイズのデータが出力されました。

なお、”\n”は改行のコードですが、以下の様にpaste()関数で文字列を結合していないため、そのまま書き出されています。この場合は、”\n”は不要です。

もし、cat(paste(“総サンプルサイズ:”, round(n_total), “\n”,”介入群のサンプルサイズ:”, round(n1), “\n”,”総サンプルサイズ:”, round(n_total),”\n”))と言うスクリプトであれば、下に示すように改行が入って出力されます。paste()関数はRの関数で文字列を結合します。sep=””と設定しないとスペース区切りになります。

それでは、今度は、lam1, lam2のハザード率の値を時間tの生存率から計算する方法をCopilotに聞いてみましょう。
lam1を介入群、lam2を対照群のハザード率とします。lam1, lam2のハザード率の値を時間tの生存率p1, p2から計算するスクリプトは?
その回答は:
以下のRスクリプトでは、介入群のハザード率を lam1、対照群のハザード率を lam2 とし、それぞれ時間 t における生存率 p1, p2 から計算します。
計算式
指数分布の性質を利用して、ハザード率は以下の式で求めます:
[ \lambda = -\frac{\ln(p)}{t} ]
ここで:
- p1 → 介入群の生存率
- p2 → 対照群の生存率
- t → 試験期間
Rスクリプト
# パラメータの設定
t <- 5 # 時間
p1 <- 0.8 # 介入群の生存率
p2 <- 0.6 # 対照群の生存率
# ハザード率の計算
lam1 <- -log(p1) / t # 介入群のハザード率
lam2 <- -log(p2) / t # 対照群のハザード率
# 結果の出力
cat("介入群のハザード率 (lam1):", lam1, "\n")
cat("対照群のハザード率 (lam2):", lam2, "\n")
ポイント
- 生存率 p が高いほど、ハザード率 λ は小さくなります。
- 時間 t が長いほど、イベント発生の確率が低いため、ハザード率は小さくなります。
p1やp2の値は 0~1 の範囲で指定する必要があります。
このスクリプトを使えば、指定した 生存率 から ハザード率 を簡単に計算できます。
試してみて、期待どおりの結果が出るかチェックしてみてください!
もしカスタマイズしたい点があれば、気軽に教えてくださいね。###ここまでCopilotの回答
確かにその通りでした。さらに、今度はハザード比を使う場合、すなわち、対照群の時間tの生存率pcで、ハザード比がhrの場合に、lam1, lam2を計算するスクリプトを聞いてみましょう。
対照群の時間tの生存率pcで、ハザード比がhrの場合に、lam1, lam2を計算するスクリプトは?
その回答は:
以下のRスクリプトでは、対照群の生存率 (pc) を基に、ハザード比 (hr) を考慮して、対照群 (lam2) と介入群 (lam1) のハザード率 を計算します。
計算式
指数分布の性質を利用して、ハザード率は以下の式で求めます:
[ \lambda_2 = -\frac{\ln(pc)}{t} ]
[ \lambda_1 = \lambda_2 \times hr ]
ここで:
pc→ 対照群の生存率hr→ ハザード比t→ 試験期間lam2→ 対照群のハザード率lam1→ 介入群のハザード率 (lam2 × hr)
Rスクリプト
# パラメータの設定
t <- 5 # 時間
pc <- 0.6 # 対照群の時間tの生存率
hr <- 0.75 # ハザード比 (介入群のリスクが対照群の75%)
# ハザード率の計算
lam2 <- -log(pc) / t # 対照群のハザード率
lam1 <- lam2 * hr # 介入群のハザード率 (ハザード比を適用)
# 結果の出力
cat("対照群のハザード率 (lam2):", lam2, "\n")
cat("介入群のハザード率 (lam1):", lam1, "\n")
ポイント
hr < 1の場合、介入群のハザード率lam1は 対照群より低く なり、リスクが低減する。hr > 1の場合、介入群のハザード率lam1は 対照群より高く なり、リスクが増加する。- 時間
tを変更すると、ハザード率のスケールが変わる。
このスクリプトで、生存率 (pc) とハザード比 (hr) から介入群・対照群のハザード率を求める ことができます。
試してみて、適切な結果が得られるか確認してみてください!
追加のカスタマイズが必要なら、気軽に教えてくださいね。###ここまでCopilotの回答
これは正しそうです。ここでRのlogは自然対数を計算します。Excelではlnです。つまり、時間tの生存率(イベント率ではありません)からハザード率を計算する式は-ln(生存率)/tです。
このサンプルサイズの計算の前提条件についてもCopilotに聞いてみましょう。
TrialSizeのTwoSampleSurvival.Equality関数によるサンプルサイズの計算の前提条件を教えてください。
TrialSize パッケージの TwoSampleSurvival.Equality 関数を用いたサンプルサイズの計算には、いくつかの前提条件があります。以下のポイントが重要です:
1. ハザード率の仮定
- 介入群(lam1)と対照群(lam2)のハザード率が指数分布に従うことが前提です。
- 比例ハザードの仮定(時間経過によってハザード比が変化しない)を満たす必要があります。
2. 有意水準(α)と検出力(1 – β)
- α(有意水準):通常 0.05 や 0.01 が使用されます。
- β(第2種過誤):一般的に 0.2(検出力80%) や 0.1(検出力90%) が選ばれます。
3. サンプルサイズ比(k)
- 介入群と対照群のサンプルサイズ比(k = n1/n2) を設定する必要があります。
- 通常は 1:1 の比率が推奨されますが、異なる比率も可能です。
4. 試験期間(ttotal)と登録期間(taccrual)
- 試験の総期間(ttotal) と 被験者登録期間(taccrual) を考慮する必要があります。
- 追跡期間が短すぎると、十分なイベント数が得られない可能性があります。
5. 患者登録の分布(gamma)
gamma = 0の場合、患者登録が一様分布であると仮定されます。gammaの値を変更することで、異なる登録パターンを考慮できます。
6. 打ち切りデータの考慮
- 観察期間内にイベントが発生しなかったデータ(打ち切りデータ) を適切に処理する必要があります。
- Coxモデルでは、打ち切りデータを考慮した解析が可能です。
これらの前提条件を満たすことで、適切なサンプルサイズを計算し、試験の統計的検出力を確保できます。さらに詳しく知りたい場合は、こちらの情報も参考になります!📊###ここまでCopilotの回答。
確かにその通りです。ハザード率が指数分布に従うというのは、例えば、1年後の生存率が0.9であれば、2年後は0.9×0.9、3年後は0.9×0.9×0.9と言う様に累乗になっていくということです。生存分析の場合、イベントは死亡です。この例では、1年後の累積イベント率(死亡率)は1 – 0.9 = 0.1で、2年後の累積イベント率は1 – 0.9×0.9 = 0.19となります。時間tにおける、死亡率がpcとすると、ハザード率 = -ln(1 – pc)/tで計算されます。1 – pcは生存率なので、生存率の自然対数に-1を掛算して、それを測定された時間で割り算するとハザード率が得られるということです。pcが対照群の時間tにおけるイベント率だとすると、このハザード率にハザード比を掛け算した値が介入群のハザード率になります。-ln(0.5)/ハザード率が生存期間中央値Median Survival Time (MST)になります。時間tをどこに設定するかは生存曲線をみて、指数関数による生存曲線ができるだけフィットしそうなところを選ぶのがひとつの方法です。
指数関数を用いる生存分析でサンプルサイズを計算するには、各群のハザード率、登録期間(Accrual time)と全試験期間(Total trial time)、α水準、βまたはPower(検出力)、そして、エントリーのパターンを指定するGammaの値が必要なことが分かります。Gammaは一定のスピードでエントリーがある場合は0ですが、引数を0にすると、分散の計算で0での割り算が生じるので、0.00001のような値を設定します。正負によって、パターンが上に凸か凹が決まります(Chow SCらの書籍を参照してください)。また、ハザード率の分散は登録期間、全試験期間とGammaによって決まります。
さて、Copilotはプログラミングに関して、かなり優れていて、有用なコードあるいはスクリプトを教えてくれます。しかし、やはり間違いが混ざることがあります。プログラムのコードの場合は、実行した際にエラーが起きる、結果が正しくないということで、間違いだということが分かるので、大きな問題は起きにくいと思われます。また、良い点としては、自分が知らない、あるいは今まで使ったことのないコードを教えてもらえるということがあります。
今後、データの変数名の設定と分析法をCopilotに伝えて、Rのスクリプトを作成させるということをいろいろ試してみたら面白いのではないかと思います。スクリプトを自分でキーボードから入力しないで済むので、それだけでも効率化が図れます。
自分があまりよく知らないことについて、Copilot、Gemini、ChatGPTに尋ねる場合は、回答をうのみにすることは避けるべきです。自分でそれが正しいかどうか判断できるものについては、効率化が図れることは間違いありません。また、自分でもあやふやな場合、その回答が正しいか何らかの方法で確かめることが必要になるでしょう。
補足:
「Copilotに2群の生存率を比較する際のサンプルサイズを計算する関数はありますか?」と聞いてみたところ、Cox.Equalityなどがあるという回答で、いろいろ聞き方をかえてもTwoSampleSurvival.Equalityはなかなか出てきませんでした。「RパッケージTrialSizeには、2つの独立した群の生存率を比較する際のサンプルサイズを計算する関数がありますか?」と聞くと、以下の様な回答で、同関数があることがやって出てきました。
Copilotの回答です:
はい、あります!TrialSizeパッケージには TwoSampleSurvival.Equality という関数があり、2つの独立した群の生存率を比較する際のサンプルサイズを計算できます。この関数は、ログランク検定を用いた生存分析に基づいて、必要なサンプルサイズを求めるのに適しています。
例えば、以下のように使用できます:
library(TrialSize)
TwoSampleSurvival.Equality(alpha = 0.05, power = 0.8, lambda1 = 0.03, lambda2 = 0.01, t = 2, sided = 2)
lambda1,lambda2は各群のイベント発生率tは観察時間alphaは有意水準powerは検出力sidedは片側/両側検定の指定
この関数を使うことで、研究の目的に応じた適切なサンプルサイズを計算できます。もしパラメータの選び方について相談があれば、お気軽にどうぞ!###Copilotの回答ここまで。
このスクリプトにはいくつか間違いがあり、このままではエラーが起きてしまいます。この関数の引数に間違いがあり、powerではなくbetaを設定する必要があり、lambda1, lambda2はそれぞれlam1, lam2です。さらに、sidedという引数はもともとありません。上記の関数のスクリプトでは、qnorm(1 – alpha/2)という計算が行われており、alphaの値を半分にしているので、Two-sidedの設定になっていることが分かります。(もしOne-sidedにしたければ2倍の値をalphaに設定する。)これはハルシネーションですね。
「RパッケージTrialSizeには、2つの独立した群のハザード率を比較する際のサンプルサイズを計算する関数がありますか?」に対しては、TwoSampleSurvival.HazardRatio関数がありますという回答でしたが、実際にはこのような関数はありません。これも、ハルシネーションですね。
また、AIは同じ質問でも、時間を変えると、違う回答のこともあります。やはり、AIの回答をそのまま100%信じるのは危険ですね。