SUCRAはNetwork Meta-analysisの結果について治療効果の順位を表す一つの指標です。累積順位曲線下面積という意味になります。それぞれの治療について累積順位確率を縦軸に順位を横軸にして描かれる曲線下の面積になるということです。
Network Meta-analysisでは3つ以上の治療法について比較することができ、その結果の一つとして 順位確率が得られます。また、統合値には間接比較の情報も取り込まれまれていますので、理論的にはペア比較のみの通常のメタアナリシスよりより確実性の高い結果が得られます。あくまで理論的にはです。
順位確率は一つの治療選択肢が1位、2位、3位…それぞれの順位になる確率を表すものです。 もしK個の治療が比較されたとすると、一つの治療について順位1からKまでの順位確率の総和は1.0になります。また それぞれの順位について全ての治療について順位確率の総和を求めるとやはり1.0になります。SUCRAはこれら順位確率の値から計算されます。
その治療法が1位になる確率、すなわち順位確率が2位以下の治療法と比べて、大きな差がある場合は、1位になる確率だけをみて、最善の治療法を選択しても問題はないと考えれらます。しかし、1位になる順位確率が次善の治療法と近い値の場合には、2位になる順位確率も考慮したほうが良いだろうということは直感的に理解できます。さらに、3位、4位、…の順位確率も全体を考慮しようとすると、SUCRAになります。
文献) Salanti G, Ades AE, Ioannidis JP: Graphical methods and numerical summaries for presenting results from multiple-treatment meta-analysis: an overview and tutorial. J Clin Epidemiol 2011;64:163-71. PMID: 20688472
下の図に 上記のSalanti Gらの論文からその計算方法を一つの例とともに示します。1位からK-1位までの累積順位確率の総和をK-1で割り算することによりSUCRAの値が得られます。SUCRAは値が100%の治療は最善であり、値が0の治療は最悪の治療と解釈されます。その値の順序は治療効果の順序を表しています。ここでは、SUCRAの値を%で表しています。計算式は図1にある通りで、順位確率から累積順位確率を求め、それらの総計をK-1で割り算するだけです。
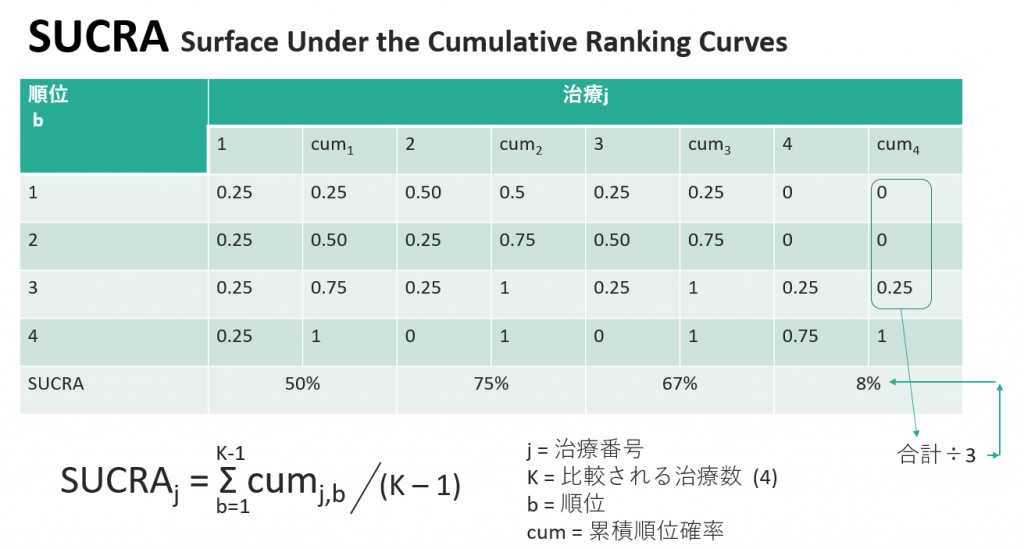
図1のSURCAをグラフ表示すると、以下のようなグラフになります。
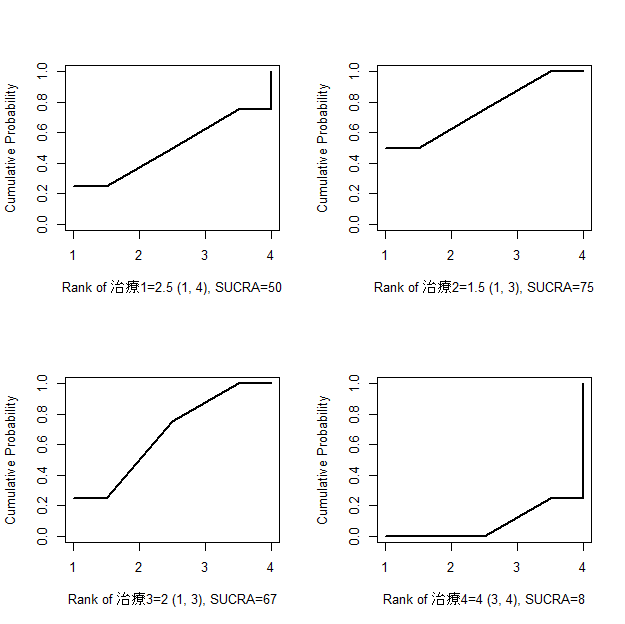
SUCRAの計算式を見ると、K-順位の値を順位確率で重みづけして、合計値を求め、最大値が100、最小値が0になるように標準化しているだけなことがわかります。K-順位の値は、1位が最大で、最下位が最小になります。
SUCRAの意味を考えてみることにします。わかりやすくするために、4頭の競走馬がそれぞれ1位から4位になる確率がわかっていて、それぞれの順位の賞金が決まっている場合、どれくらいのリターンが得られといえるか考えてみます。図3にデータを示します。
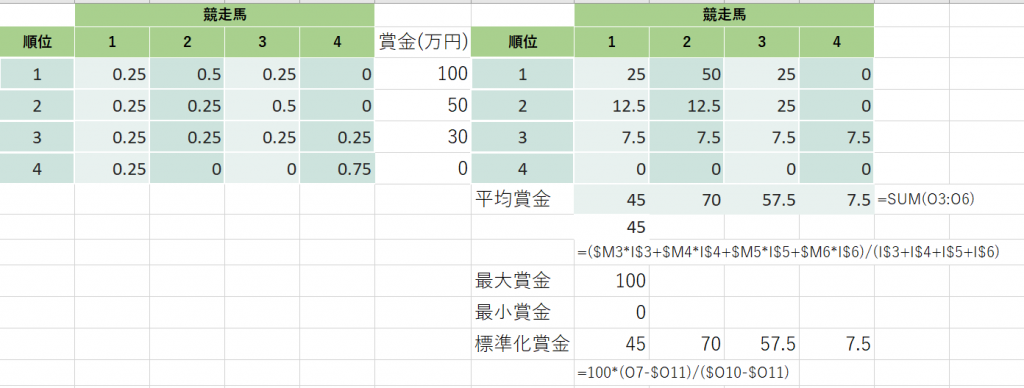
順位確率の値は、図1の場合と同じにしました。ざっと眺めると、1位の確率が一番高いのは競走馬2です。競走馬4が最下位の確率が一番高いこともわかります。
まず左側の順位確率にそれぞれの賞金の額を掛け算した値を計算します。たとえば、競走馬1は25, 12.5, 7.5, 0となります。もし競走馬1が1位になったら、100万円の賞金が獲得できるわけですが、1位の確率は0.25なので、100×0.25=25万円が現在の価値です。もし2位になったら50万円の賞金が獲得できるわけですが、2位の確率は0.25なので、50×0.25=12.5万円が現在の価値です。3位、4位も同様に計算します。
確率で考えるとわかりにくい場合は、次のように考えてみてください。この表に示す競走馬1の場合、これらの確率で起きる事象を何回も繰り返すと、例えば、100万回繰り返すと、1位になるのが25万回、2位になるのが25万回、3位になるのが25万回、4位になるのが25万回にになるはずです。多項分布に従うので、回数が少ないともっとばらつきますが、100万回も繰り返せば、まずこうなるでしょう。さて、100万回競走馬1にかけた場合、獲得賞金の平均は、(100×25万+50×25万+30×25万+0×25万)/(25万+25万+25万+25万)=45万円です。
分かりやすくするために、100万回繰り返した場合を考えて計算しましたが、もともと順位確率を競走馬それぞれで合計すると1.0になるので、単純に先に計算した順位確率で重みづけした賞金金額を合計する、つまり25+12.5+7.5+0 = 45万円が競走馬1の予想獲得金額、いいかえると現在の価値となります。
さらに、予想される最高獲得金額は1位になった場合の、100万円、最小獲得金額は4位になった場合の0円なので、これら最大値、最小値を用いて標準化してみます。図3の右下の標準化賞金のところに書いてある計算式で計算します。つまり、予想獲得金額から最小値を引き算した値を、最大値から最小値を引き算した値で割り算し、%にするため100を掛け算します。この値は、最大で100、最小で0となります。各競走馬の標準化賞金を見ると、競走馬2が70万円で最高になります。この例では、1位の賞金が100、4位の賞金が0にしてあるので、平均賞金と標準化賞金が同じ額になっています。
それでは、賞金金額を先ほどのSUCRA計算時に使ったK-順位の値に置き換えて同じように計算してみます。1位から4位までの価値を3,2,1,0と設定することになります。平均価値は上記の平均賞金、標準化価値は同じく標準化賞金と同じ計算法です。
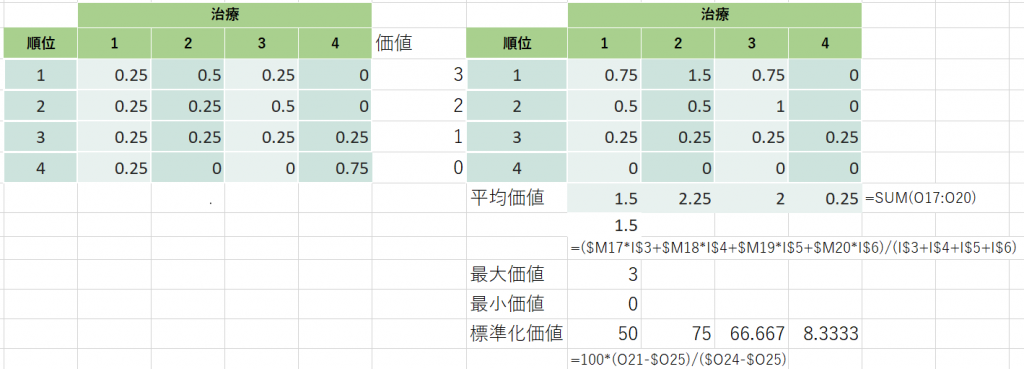
標準化価値はSUCRAと同じ値になります。SUCRAの計算はそれぞれの順位の価値をそれぞれの順位になる確率で重みづけした平均値と同じだということがわかります。それでは、なぜ、価値を3,2,1,0にする必要があるのでしょう?これを4,3,2,1に変えて同じ計算をやってみます。

標準化価値の値は全く同じです。SUCRAの計算はこのやり方でも算出できることがわかります。つまり、順序が同じで、間隔が同じ値を設定すると、SUCRAの値が計算できるということです。それでは、価値の値を100,80,60,40にしたらどうなるでしょうか。

図6の示すように、標準化価値はSUCRAと全く同じ値です。
それでは、順序は同じだが、間隔は異なる値を価値に設定したらどうなるか見てみましょう。
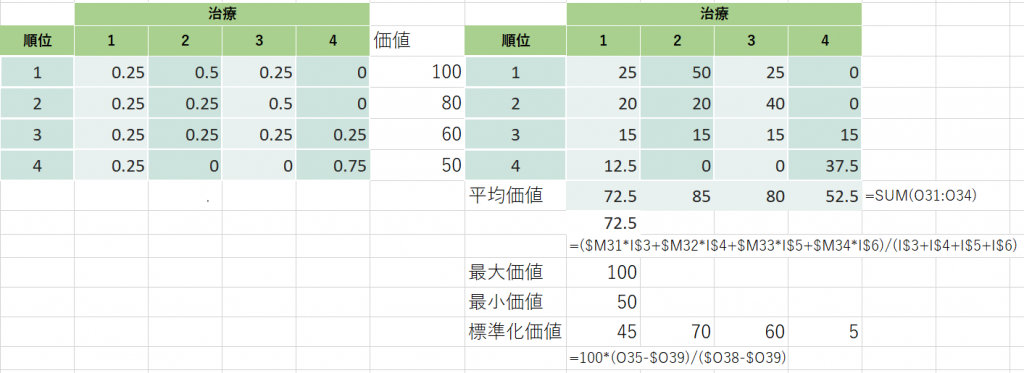
標準化価値は違う値になります。ただし、上下関係は変わりません。SUCRAは順位だけを問題にしているので、図1に示すような計算でいいのですが、1位と2位になった場合の絶対効果の大きさは違います。もしその治療が2位になったら、他の治療が1位になり、その治療のほうが効果が大きいはずです。
もし、各治療の絶対効果の大きさをK-順位のかわりに用いたら、順位は同じになりますが、それぞれの治療で得られるであろう絶対効果の大きさは異なる印象を与えかもしれません。たとえば、図7に示す例では、標準化する前の平均価値はSUCRAでは1位になる治療2が85、同じく2位になる治療3が80で大きな差は無いと思われます。
また、標準化する前の平均価値は最下位の価値を0にする場合と、そうでない場合で異なってきます。SUCRAは最下位を0にするので、それがプラセボや無治療であればいいのかもしれませんが、アクティブな治療の場合は、平均価値を0にすることに違和感があります。
順序変数は間隔が同じでないということがここには表れているとも言えます。順位は順序変数である、つまり1位と2位の間隔と2位と3位の間隔は必ずしも同じではないということです。
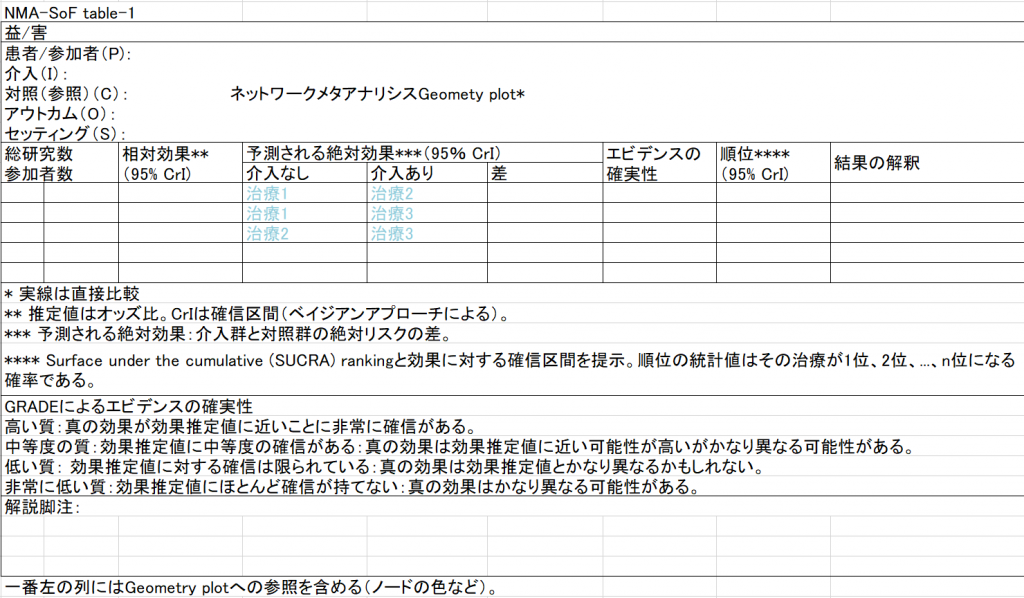
さて、GRADE approachではネットワークメタアナリシスのSoF (Summary of Findings) tableにはSUCRAを記述する欄があります。したがって、SURCRAの計算が必要になります。
文献)Yepes-Nuñez JJ, Li SA, Guyatt G, Jack SM, Brozek JL, Beyene J, Murad MH, Rochwerg B, Mbuagbaw L, Zhang Y, Flórez ID, Siemieniuk RA, Sadeghirad B, Mustafa R, Santesso N, Schünemann HJ: Development of the summary of findings table for network meta-analysis. J Clin Epidemiol 2019;115:1-13. PMID: 31055177