Copilotに聞きながら、ベイジアンアプローチのメタアナリシスを実行するスクリプトやコードを書けるか試してみたいと思います。
ベイジアンアプローチによる統計解析は、OpenBUGSやJAGSでMarkov Chain Monte Carlo (MCMC) simulationを行って、データから事後分布を推定する解析手法です。頻度論派frequentistの伝統的な統計学による方法よりも、より簡単に複雑なモデルを扱うことができるとされています。MCMCの方法はいくつか考案されていますが、OpenBUGSやJAGSの方法はGibbs samplerです。
メタアナリシスにおいても、今までOpenBUGSやJAGSを使う方法がペア比較のメタアナリシス、ネットワークメタアナリシスで利用されてきました。例えば、ネットワークメタアナリシス用のRのパッケージであるgemtcやpcnetmetaはJAGSを用いています。Rとの連携はrjagsが使われており、フォレストプロットなども出力できます。
それではまず、OpenBUGSやJAGS以外にRでMCMCを実行する方法があるか聞いてみましょう。
Copilotの回答は青いブロックの右端のアイコンをクリックすると表示したり隠したりできます。
RでOpenBUGSやJAGS以外にベイジアンアプローチの解析でMarkov Chain Monte Carlo (MCMC) simulationを実行する方法はありますか?
はい、OpenBUGSやJAGS以外でも、RでMCMCシミュレーションを実行する方法はいくつかあります。代表的なものを紹介します:
- Stan (
rstanパッケージ)- Hamiltonian Monte Carlo (HMC) を使用し、より効率的なMCMCサンプリングを実現します。
rstanを使えば、StanのモデルをRで簡単に扱えます。- 収束が速く、複雑なベイジアンモデルにも適しています。
- MCMCpack (
MCMCpackパッケージ)- 一般的なベイジアン統計モデルのMCMC推定を簡単に実行できます。
- 事前分布を指定し、MCMCを用いた推定を行うことが可能です。
- nimble (
nimbleパッケージ)- BUGSのようなモデル記述をサポートしつつ、カスタムMCMCアルゴリズムを作成できます。
- 高速な計算が可能で、柔軟なモデリングができます。
- BayesianTools (
BayesianToolsパッケージ)- MCMCのほか、SMC(Sequential Monte Carlo)などのベイジアン推論手法を提供します。
- モデル適合性の評価や事後分布の解析が容易です。
Stanは特に強力で、最近のベイジアン解析では広く使われています。どれか試してみたいものはありますか?
詳細なチュートリアルやサンプルコードが必要なら、お知らせください!
Rでrstanを介して、Stanを動かし、Gibbs samplerではなく、Hmiltonian Monte Carlo (HMC)を使ったMCMCで、より効率的なサンプリングができるらしいことが分かりました。
そこで、Stanをメタアナリシスに使用した報告があるか聞いてみましょう。
メタアナリシス、ネットワークメタアナリシスでStanを使った報告は多いですか?
はい、Stanはメタアナリシスやネットワークメタアナリシスで広く使用されています。Stanの公式ユーザーガイドにもメタアナリシスのセクションがあり、ベイジアンアプローチの適用方法が詳しく説明されています。
また、Stanを用いたネットワークメタアナリシスに関する報告も増えており、特に従来のWinBUGSやJAGSと比較して、より高速で収束しやすい点が評価されています。日本語の解説もあり、Stanを使ったネットワークメタアナリシスの実装例が紹介されています。
StanはHMC(Hamiltonian Monte Carlo)を採用しているため、従来のMCMCよりも効率的にサンプリングできるのが特徴です。これにより、複雑なメタアナリシスモデルでも安定した推定が可能になります。Stanを使ったメタアナリシスに興味があれば、公式ドキュメントや関連論文をチェックしてみると良いですね!
何か具体的なモデルについて知りたいことはありますか?
参照できるような情報がかなりあるようです。そして、StanはOpenBUGSやJAGSよりも高速で収束しやすいという利点があるようです。そこで、RでStanを動かすために、必要なパッケージをインストールするためのスクリプトを提案してもらおうと思います。すでにインストール済みのパッケージは除き、OSはWindows11にします。
RでStanを使ったベイジアンアプローチのメタアナリシスをしたいと思います。 インストール済みのパッケージ以外のインストールをJapanのミラーサイトから行うRのスクリプトは? OSはWindows11です。
Windows 11環境で、すでにインストール済みのパッケージを確認しつつ、足りないものを日本のCRANミラーサイトからインストールするRのスクリプトはこちらです:
# 必要なパッケージのリスト
packages <- c("rstan", "Rcpp", "ggplot2", "coda")
# CRANの日本ミラーサイトを指定
chooseCRANmirror(graphics = FALSE, ind = 68) # 68番はJapanのミラー
# インストールされていないパッケージを探す
missing_packages <- setdiff(packages, rownames(installed.packages()))
# 足りないパッケージだけインストール
if(length(missing_packages) > 0) {
install.packages(missing_packages)
}
# Stanコンパイラの設定(初回のみ)
Sys.setenv(USE_CXX14 = 1)
このスクリプトでは、installed.packages()を使って既にインストール済みのパッケージを確認し、未インストールのものだけをCRANの日本ミラーサイトからインストールするようにしています。
これでスムーズにStanを使ったベイジアンメタアナリシスの環境が整うはずです。何か追加の設定が必要になれば、気軽に聞いてください!
提案されたスクリプトをそのままコピーして、実行したところ、問題なく必要なパッケージをインストールできました。
Stanコンパイラの設定(初回のみ)というスクリプトがあります。このスクリプトの意味を聞いてみましょう。
Stanコンパイラの設定(初回のみ)のスクリプトの目的は?
Sys.setenv(USE_CXX14 = 1) の設定は、Stanを正しくコンパイルするために必要な環境変数を設定する役割を果たします。
StanはCで書かれた統計モデリング言語であり、rstan パッケージを使用する際には、適切なCコンパイラの設定が重要になります。特に、Windows環境では適切なコンパイルオプションを指定しないと、Stanモデルのコンパイル時にエラーが発生する可能性があります。
このスクリプトの目的は:
- C++14を有効化 – Stanの最新バージョンではC++14以降が必要なため、環境変数
USE_CXX14=1を設定します。 - モデルのスムーズなコンパイル – この設定を行うことで、Stanコードを正しくコンパイルできるようになります。
この設定は通常、Rセッションの最初に一度だけ行えば十分です(毎回実行する必要はありません)。ただし、環境設定がリセットされた場合や、新しいRセッションを開始した場合には再設定が必要になることもあります。
もしコンパイル時に問題が発生する場合は、rstan の公式ドキュメントを確認するか、追加の設定が必要かどうか調べるのも良いですね。何か困ったことがあれば、いつでも聞いてください!
Copilotの回答は、StanはC言語で書かれており、StanのモデルをコンパイルするためのC++14を有効化することだという説明です。また、このスクリプトの実行は初回のみ必要だということです。Rでrstanをインストールすると、Stanも一緒にインストールされるようです。私の場合は、rstan以外のパッケージはインストール済みでしたので、rstanだけが新たにインストールされました。
それでは、二値変数アウトカムで、ペア比較メタアナリシスを実行し、リスク比の統合値と95%信頼区間を計算するスクリプトを提案してもらいましょう。変数名は指定します。
rstanをインストール後、二値変数アウトカムの場合のペア比較メタアナリシスを実行したいと思います。簡単なサンプルデータと、リスク比の統合値と95%信頼区間を計算するスクリプトを提案してください。研究IDの変数はstudy、対照群の症例数はnc、イベント数はrc、介入群の症例数はnt、イベント数はrtとします。
了解しました。以下のスクリプトでは、rstan を使用してペア比較メタアナリシスを実行し、リスク比 (Risk Ratio, RR) の統合推定値とその95%信頼区間を計算します。
1. サンプルデータの作成
まず、指定された変数 study, nc, rc, nt, rt を含むデータを作成します。
# 必要なパッケージをロード
library(rstan)
# サンプルデータ
meta_data <- list(
N = 5, # 研究数
study = 1:5, # 研究ID
nc = c(100, 200, 150, 120, 250), # 対照群の症例数
rc = c(10, 30, 20, 15, 25), # 対照群のイベント数
nt = c(100, 200, 150, 120, 250), # 介入群の症例数
rt = c(15, 40, 22, 18, 35) # 介入群のイベント数
)
2. Stanモデルの定義
Stanのコードを記述し、リスク比のログ値 (logRR) を推定します。
data {
int<lower=1> N;
int nc[N];
int rc[N];
int nt[N];
int rt[N];
}
parameters {
real logRR[N]; # リスク比の対数値
real mu; # リスク比の統合値(対数)
real<lower=0> sigma; # 研究間のばらつき
}
model {
# 事前分布
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
# 各研究のリスク比推定
for (i in 1:N) {
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], inv_logit(0)); # 対照群
rt[i] ~ binomial(nt[i], inv_logit(logRR[i])); # 介入群
}
}
3. Stanモデルの実行
RからStanモデルを実行し、リスク比とその95%信頼区間を計算します。
# Stanモデルのコンパイルと実行
fit <- stan(
model_code = stan_model_code,
data = meta_data,
iter = 2000, chains = 4
)
# 推定結果の抽出
posterior_samples <- extract(fit)
mu_samples <- posterior_samples$mu
# リスク比 (exp(mu)) と 95% 信頼区間の計算
risk_ratio <- exp(mean(mu_samples))
conf_int <- exp(quantile(mu_samples, probs = c(0.025, 0.975)))
# 結果の表示
cat("推定されたリスク比:", risk_ratio, "\n")
cat("95% 信頼区間:", conf_int[1], "-", conf_int[2], "\n")
まとめ
このスクリプトでは、
✅ ペア比較メタアナリシスをStanで実行
✅ リスク比 (RR) の統合値を推定
✅ 95% 信頼区間の計算
Stanは高速なMCMCを用いるため、収束が速く、従来のBUGS系よりも精度の高い推定が可能です。
さらにカスタマイズしたい点があれば、教えてください!
まずは、提案されたRのスクリプトをそのまま実行してみようと思いますが、実際やってみると、2. Stanモデルの定義のスクリプトの実行でエラーが起きました。そのエラーの最初の部分だけを下に示します。

この部分のスクリプトはモデルの記述で、おそらくStanで実行されるdataとparametersとmodelが記述されている部分だろうと思われます。Stanが実行するコードですから、それをそのままRで実行しようとしてもエラーが起きるのは当然と言えるでしょう。
そこで、正しい記述法をCopilotに提案してもらいましょう。
Stanのモデルの定義をRでそのまま実行するとエラーが起きます。data, parameters, modelの正しい記述法は?
StanのコードをRで正しく扱うためには、Stanのモデルを.stanファイルに保存するか、文字列としてR内に記述する必要があります。
また、stan()関数でモデルを実行する際には、適切なデータ構造を指定することも重要です。
1. Stanコードの記述
Stanのモデル定義は 文字列として保存 し、stan_model_code に格納します。
stan_model_code <- "
data {
int<lower=1> N;
int nc[N];
int rc[N];
int nt[N];
int rt[N];
}
parameters {
real logRR[N];
real mu;
real<lower=0> sigma;
}
model {
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
for (i in 1:N) {
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], inv_logit(0));
rt[i] ~ binomial(nt[i], inv_logit(logRR[i]));
}
}
"
この方法でStanコードをR内に保存できます。
2. データの準備
Stanモデルに渡すデータは、リスト形式 にする必要があります。
meta_data <- list(
N = 5,
nc = c(100, 200, 150, 120, 250),
rc = c(10, 30, 20, 15, 25),
nt = c(100, 200, 150, 120, 250),
rt = c(15, 40, 22, 18, 35)
)
3. Stanモデルの実行
stan()関数を使ってモデルを実行します。
library(rstan)
fit <- stan(
model_code = stan_model_code,
data = meta_data,
iter = 2000, chains = 4
)
print(fit)
エラー回避ポイント
- Stanコードは文字列として格納 (
stan_model_code <- "...") - データはリスト形式 (
meta_data <- list(...)) - Stanのモデルは
stan()関数で実行
この方法でエラーなくStanのモデルを実行できるはずです。
もしまだエラーが出る場合は、詳細を教えてください!
回答では、サンプルデータの作成のスクリプトは同じままでした。Stanコードの記述がstan_model_codeという変数に文字列として格納するように書き換わっています。Stanで実行されるコードはdata, parameters, modelの3つの要素からなり、それぞれテキストとして記述されるということが分かります。またmodelの部分をテキストファイルとして保存して、実行の際にそれを読み込んで使用することもできるようですが、それは後で試すことにして、Rのスクリプトの中で、stan_model_codeという変数に直接格納することにします。
1.Stanコードの記述の部分を見ると、dataの部分はintegerすなわち、整数で配列構造で整数Nが順番を表すという形式であることを示しています。parametersの部分はmodelでの計算に使われる変数を実数として宣言しています。そしてmodelでは、muは平均値0、標準偏差10の正規分布、sigmaは位置0、スケール2のCauchy distributionコーシー分布からサンプリングすることが定義されています。これら事前分布はかなり幅の広い、あいまい分布になります。
さらに、log(RR)が平均値mu, 標準偏差sigmaの正規分布からサンプリングすること、rc[i], rt[i]すなわちイベント数は二項分布からサンプリングすることが定義されています。
Stanモデルの実行のスクリプトは最初の提案と同じですが、今回のCopilotの回答には、推定結果の抽出と結果の表示の部分のスクリプトは含まれていませんでした。
- それではまず、Stanコードの記述の部分を実行してみます。今度はエラーは起きません。つまり、Stanで使われる、stan_model_codeという変数に、data, parameters, modelの3要素が格納されたようです。
modelの設定に続いて、最初のCopilotの提案の、Stanモデルの実行のスクリプトを実行してみます。やはりエラーが起きてしまいました。WARNINGが出力され、Rtoolsをインストールする必要があるとのメッセージです。

そこでWARNINGの中ののURL https://cran.r-project.org/bin/windows/Rtools/を開いてみたところが以下の図です。Rのバージョンによって異なるプログラムが用意されています。
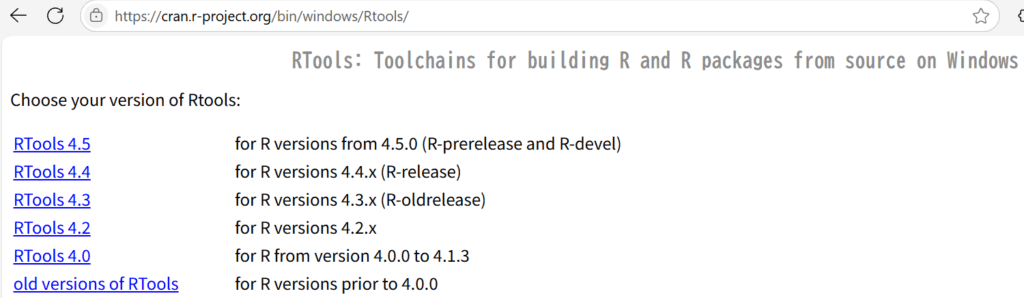
今このPCで使用しているRはVersion 4.4.3なので、RTools 4.4をインストールしてみます。RTools 4.4をクリックすると以下の解説があります。
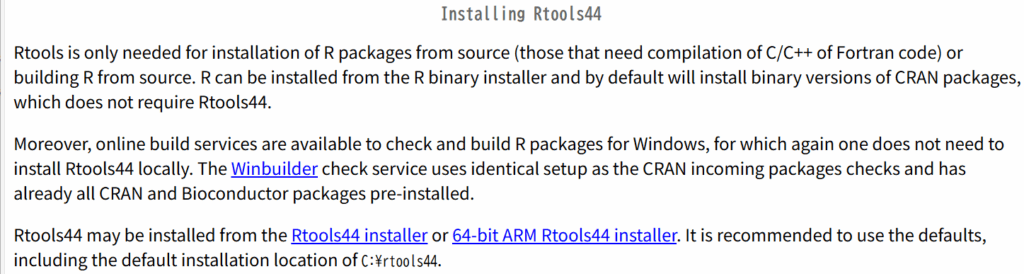
インストールを実行する前にCopilotに聞いて確認しておきましょう。
Stanモデルの実行で、RToolsのインストールが必要だというWARNINGが出ました。
StanのモデルをWindows環境で実行するには、RTools のインストールが必要です。RToolsは、StanのC++コンパイルをサポートするツールチェーンであり、rstan を正しく動作させるために必要になります。
RToolsのインストール方法
- RToolsの公式サイトから最新版をダウンロードします → こちら
- インストーラーを実行し、デフォルト設定でインストールします。
- インストール後、Rを再起動し、以下のコマンドでRToolsが正しく認識されているか確認します:
system("g++ -v") # C++コンパイラのバージョン確認 system("where make") # makeコマンドの確認これらのコマンドが正常に動作すれば、RToolsのインストールは成功しています。
RToolsをStanで使用するための設定
Stanを正しく動作させるために、以下の設定を行います:
install.packages("Rcpp", type = "source") # C++インターフェース
install.packages("inline", type = "source") # Stanのコンパイル補助
これでStanのモデルをスムーズに実行できるはずです。
もし追加のエラーが発生した場合は、詳細を教えてください!
以上を確認したうえで、RTools installer 4.4をダウンロードし、デフォルトの設定でインストールを実行しました。431MBのかなり大きなプログラムなのでダウンロードには少し時間がかかりました。RToolsのインストーラーのダウンロードが終了したら、いったんRを閉じて、ダウンロードしたrtools44-6459-6401.exeファイルをダブルクリックしてインストールしました。

Copilotの回答には、Rを再起動し、system(“g++ -v”)およびsystem(“where make”)を実行してインストールが成功したか確認するとあったので、それを実行してみました。
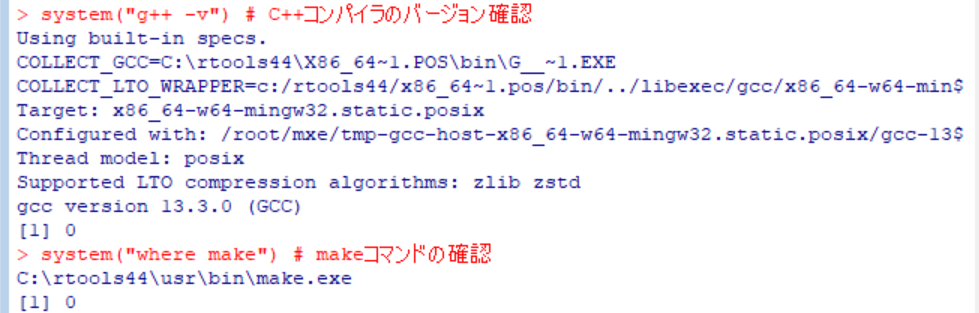
特にエラーメッセージは出ませんでした。
そこで、再度最初から以下を実行してみました。
サンプルデータmeta-dataの作成、stan_model_codeの作成、そして続けて、Stanモデルのコンパイルと実行です。その結果、コンソールにはChain 1~4までのWarmup、Samplingの結果が出力されました。Chain 1の部分を以下に示します。一つのチェーンで最初の1000回はウォームアップ、残り1000回はサンプリングのデータを保存したということです。チェーン1で0.101秒かかっていました。
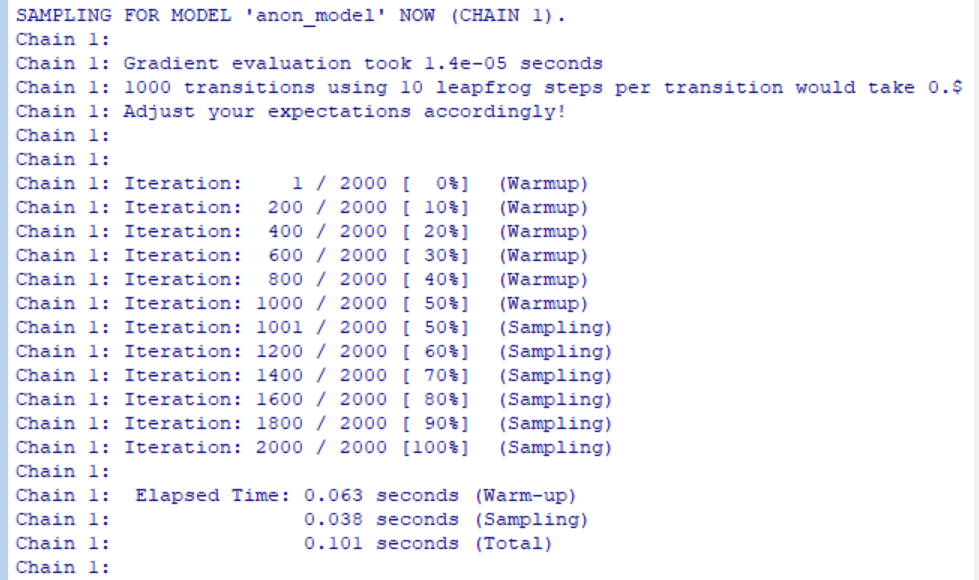
上記の最初のCopilotの提案の内、3.Stanモデルの実行の# 推定結果の抽出、# リスク比 (exp(mu)) と 95% 信頼区間の計算、# 結果の表示の部分を実行しました。
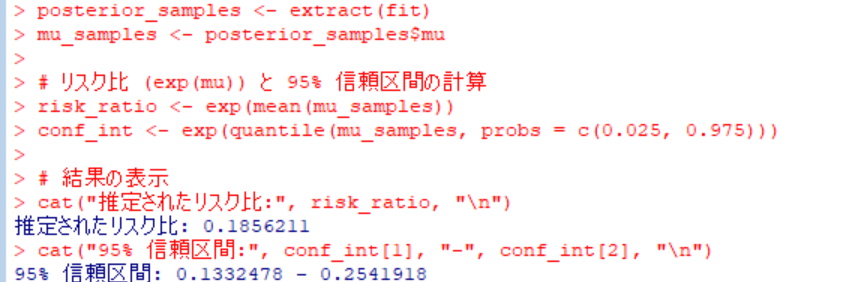
リスク比の統合値と95%信頼区間の値が出力されていました。
しかし、このリスク比の統合値は正しいとは思えません。なぜなら、解析対象のデータを見ると、nc, ntつまり対照群と介入群の症例数は同数で、どの研究もrt > rcつまりイベント数は介入群の方が対照群より大きい値です。ですから、リスク比は1.0より大きくなるはずですが、統合値は0.185となっているので、明らかに間違っています。
そこで、modelをよく見ると、以下の様にrc[i] ~ binomial(n[i], inv_logit(0));の部分がどうもおかしいようです。
model {
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
for (i in 1:N) {
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], inv_logit(0));
rt[i] ~ binomial(nt[i], inv_logit(logRR[i]));
}
}
Stanのinv_logit()関数についてCopilotに聞いてみました。
Stanのinv_logit()関数はどのような演算をするのでしょうか?
Stanのinv_logit()関数は、ロジスティック関数(シグモイド関数)を計算するための関数です。これは、入力値を0から1の範囲に変換する役割を持ちます。
定義
inv_logit(x) は、以下の式で計算されます:
[ \text{inv_logit}(x) = \frac{1}{1 + e^{-x}} ]
この関数は、ロジスティック回帰やベイジアン統計モデルで確率の推定に広く使われます。
特徴
✅ 入力値が負の値 → 出力は 0 に近づく
✅ 入力値が 0 → 出力は 0.5
✅ 入力値が正の値 → 出力は 1 に近づく
Stanでは、inv_logit() を使って確率を表す変数を定義することが多いです。例えば、ロジスティック回帰モデルでは以下のように使用されます:
parameters {
real beta;
}
model {
beta ~ normal(0, 1);
real p = inv_logit(beta); // 確率の計算
}
Stanの公式ドキュメントにも詳しい説明がありますので、さらに詳しく知りたい場合はこちらをチェックしてみてください!💡
つまり、inv_logit()関数はロジスティック回帰で従属変数の値から確率の値を求める際の計算式と同じで、1/(1 + exp(-x))を計算する関数です。inv_logit(0)は0.5になり、対照群のイベント率がいつも0.5に固定されてしまいます。
そこで、この間違いを指摘ながら、正しいと思われるスクリプトをCopilotに提案してもらおうと思います。
以下のコードはStanで二値変数アウトカムのメタアナリシスを実行するコードです。ncは対照群の症例数、rcは対照群のイベント数、ntは介入群の症例数、rtは介入群のイベント数です。効果指標はリスク比を用います。このコードの中で、rc[i] ~ binomial(nc[i], inv_logit(0)); は正しいですか?inv_logit(0)は0.5に固定されるので、対照群のイベント率が0.5に固定されてしまいます。
<以下上記のモデルのコードをここに記述>
はい、ご指摘の通り、inv_logit(0) は 常に 0.5 となるため、このコードでは対照群のイベント率が 0.5 に固定されてしまいます。これは、研究ごとのイベント率のばらつきを考慮していないため、不適切な設定になっています。
修正方法
対照群のイベント率をデータに基づいて推定できるようにするため、rc[i] の分布を binomial() に渡す確率 ( p_c[i] ) をデータから取得する形に修正しましょう。
修正後のStanモデル
data {
int<lower=1> N;
int nc[N];
int rc[N];
int nt[N];
int rt[N];
}
parameters {
real logRR[N]; // リスク比の対数値
real mu; // リスク比の統合値(対数)
real<lower=0> sigma; // 研究間のばらつき
real p_c[N]; // 対照群のイベント率
}
model {
# 事前分布
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
# 対照群のイベント率の事前分布(ベータ分布を使用)
for (i in 1:N) {
p_c[i] ~ beta(1, 1); // 一様な事前分布
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], p_c[i]); // 修正
rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i])); // 介入群
}
}
修正のポイント
- イベント率
p_c[i]をパラメータとして推定p_c[i] ~ beta(1, 1);で 一様な事前分布 を設定(研究ごとの不確実性を考慮)
- 対照群のイベント率
p_c[i]をbinomial()に適用rc[i] ~ binomial(nc[i], p_c[i]);- 各研究のイベント率 を適用することで、固定値
0.5ではなく、データに基づいた推定が可能に
- 各研究のイベント率 を適用することで、固定値
- 介入群のイベント率を
p_c[i] * exp(logRR[i])にrt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i]));- リスク比
exp(logRR[i])を適用 してイベント率を調整
- リスク比
この修正のメリット
✅ イベント率のばらつきを考慮した推定が可能
✅ 対照群のイベント率を固定値 0.5 にする問題を解消
✅ ベイジアンアプローチに適した柔軟な推定ができる
この修正が適切かどうか、試してみてください!もしさらに調整が必要なら、お知らせください💡
この修正されたコードをもう一度実行してみましょう。修正後のStanモデル全体をダブルクォーテーションで囲み、変数stan_model_codeに格納します。
さて、この修正モデルを実行するとstan()関数の実行の所で、初期値が扱える範囲外であるというエラーが多発しました。
そこで、そのエラーメッセージに対する対処をCopilotに聞いて、2回ほど修正を加え、実行可能とだったスクリプトは以下の通りです。この部分のCopilotとのやりとりは省略します。
#Fixed effects model with binoial distributions:
# 必要なパッケージをロード
library(rstan)
# サンプルデータ
meta_data <- list(
N = 5, # 研究数
study = 1:5, # 研究ID
nc = c(100, 200, 150, 120, 250), # 対照群の症例数
rc = c(10, 30, 20, 15, 25), # 対照群のイベント数
nt = c(100, 200, 150, 120, 250), # 介入群の症例数
rt = c(15, 40, 22, 18, 35) # 介入群のイベント数
)
stan_model_code <- "data {
int<lower=1> N;
int nc[N];
int rc[N];
int nt[N];
int rt[N];
}
parameters {
real logRR[N]; // リスク比の対数値
real mu; // リスク比の統合値(対数)
real<lower=0> sigma; // 研究間のばらつき
real<lower=0, upper=1> p_c[N]; // 確率値の制約を追加
}
model {
# 事前分布
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
# 対照群のイベント率の事前分布(ベータ分布を使用)
for (i in 1:N) {
p_c[i] ~ beta(1, 1); // 一様な事前分布
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], p_c[i]); // 修正
rt[i] ~ binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1)); // 最大値を1に制限
}
}"
rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i])); // 介入群
N=meta_data$N
init_values <- function() {
list(mu = 0, sigma = 1, logRR = rep(0, N), p_c = rep(0.1, N)) # 確率の初期値を設定
}
# Stanモデルのコンパイルと実行
fit <- stan(model_code = stan_model_code, data = meta_data, init = init_values, iter = 2000, chains = 4)
# 推定結果の抽出
posterior_samples <- extract(fit)
mu_samples <- posterior_samples$mu
# リスク比 (exp(mu)) と 95% 信頼区間の計算
risk_ratio <- exp(mean(mu_samples))
conf_int <- exp(quantile(mu_samples, probs = c(0.025, 0.975)))
# 結果の表示
cat("推定されたリスク比:", risk_ratio, "\n")
cat("95% 信頼区間:", conf_int[1], "-", conf_int[2], "\n")
######Copilotが提案したコードはFixed effects modelだと記されていますが、modelを見るとlogRR[i] ~ normal(mu, sigma)となっていて、各研究のリスク比の自然対数を平均値mu、標準偏差sigmaの正規分布からサンプリングしているので、これはRandom effects modelのはずです。そして、stan_model_codeに格納されるmodelの記述の中にあるrt[i] ~ binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1));がその下に重複して記述されています。これは間違いと思われるので、Copilotに聞いてみましょう。
これはStan, rstanでペア比較メタアナリシスを実行するためのRのスクリプトです。 これはFixed effects modelではなくRandom effects modelではないでしょうか。 ダブルクォーテーションで囲ったmodelの記述の後の以下の部分は必要ですか? rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i])); // 介入群
<以下スクリプト全体のコピー>
このStanのコードはRandom effects modelに該当します。理由としては、以下の点が挙げられます:
logRR[i] ~ normal(mu, sigma);の部分で、各研究の対数リスク比logRR[i]が全体の平均muと研究間のばらつきsigmaに従う正規分布から生成されているため、個々の研究のリスク比が異なる可能性を考慮していることになります。これはRandom effects modelの特徴です。- Fixed effects modelでは、
logRR[i]は各研究で固定された値を持つべきですが、このモデルでは研究間のばらつきを考慮して正規分布に基づく変動を許容しているため、Random effects modelと言えます。
次に、rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i])); の部分ですが、これは介入群のイベント発生数 rt[i] を確率 p_c[i] * exp(logRR[i]) に基づく二項分布から生成している処理です。このコードは必要であり、介入群のイベント率をモデル化する重要な式になっています。
ただし、p_c[i] * exp(logRR[i]) が1を超える可能性があるため、後の修正では fmin(p_c[i] * exp(logRR[i]), 1) を使用して確率の上限を1に制限しています。この修正は適切であり、数値的な不安定さを防ぐために重要です。
もしFixed effects modelにしたい場合は、logRR[i] を変数として個別に推定するのではなく、全ての研究で共通の logRR を固定する形に書き換えると良いでしょう。たとえば、logRR[i] ~ normal(mu, 0.001); のように sigma をほぼゼロにすることで、変動を抑えられます。
何か他に修正点や疑問があれば、お気軽に聞いてください!
やはりRandom effects modelです。そして、Fixed effects modelにしたい場合のlogRR[i]のサンプリングの方法が提案されています。
rt[i] ~ binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1));の重複については、必要だとの回答ですが、もう一度確認してみましょう。
stan_model_codeに格納される””内のコードにrt[i] ~binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1)); // 最大値を1に制限があるので、その下にある同様のコードは不要では?
その通りです!stan_model_code に格納されるStanのコード内で、rt[i] ~ binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1)); の記述があるため、 その後の rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i])); は不要です。
重複したコードを削除しても問題なく動作するはずですし、余計な記述がなくなることでコードの可読性も向上します。特に、確率値の上限を1に制限する修正がすでに適用されているため、後ろのコードをそのまま残すと、制約なしの二項分布に戻ってしまう可能性があるので注意が必要です。
他にもコードの整理や最適化について相談があれば、お気軽に聞いてください!
やはり不要の様です。
また、このコードには初期値に関する設定が含まれていました。それが必要なのか聞いてみましょう。
init_values <- function(){ }の部分は必要ですか?
init_values <- function(){ } の部分は必須ではありませんが、モデルの収束を安定させるために役立つ場合があります。
この関数は、StanのMCMC(マルコフ連鎖モンテカルロ)サンプリングを開始するときに初期値を設定するためのものです。特に、Stanのデフォルトの初期化では、パラメータにランダムな値を割り当てるため、時々収束の問題が発生することがあります。これを防ぐために、init_values を定義して適切な初期値を設定することで、よりスムーズに計算が進む可能性があります。
ただし、もし init_values を削除してもモデルが問題なく収束するなら、必須ではないので省略できます。より安定した推定を得たい場合は、適切な初期値を設定することをおすすめします。
他にも気になる点があれば聞いてください!
確かに、初期値の設定は必須ではないのですが、時にMCMCが収束しない問題を避けるため適切な初期値を設定することが望ましいです。この例では、muに0、sigmaに1、logRRにN個の研究すべて0、p_cすなわち対照群のイベント率にN個の研究すべてに0.1を設定するようになっています。
そのほかスペルミスもあったので、それらも含めて修正したコードを書き出してもらいましょう。
それでは、Random effects modelに修正、binoial distributionsをbinomial distributionsに修正、コードの重複部分を削除したコードを書き出してください。
了解しました!以下のコードでは、Random effects model に修正し、binomial distributions のスペルミスを修正し、重複部分を削除しました。
# 必要なパッケージをロード
library(rstan)
# サンプルデータ
meta_data <- list(
N = 5, # 研究数
study = 1:5, # 研究ID
nc = c(100, 200, 150, 120, 250), # 対照群の症例数
rc = c(10, 30, 20, 15, 25), # 対照群のイベント数
nt = c(100, 200, 150, 120, 250), # 介入群の症例数
rt = c(15, 40, 22, 18, 35) # 介入群のイベント数
)
stan_model_code <- "data {
int<lower=1> N;
int nc[N];
int rc[N];
int nt[N];
int rt[N];
}
parameters {
real logRR[N]; // リスク比の対数値
real mu; // リスク比の統合値(対数)
real<lower=0> sigma; // 研究間のばらつき
real<lower=0, upper=1> p_c[N]; // 確率値の制約を追加
}
model {
// 事前分布
mu ~ normal(0, 10);
sigma ~ cauchy(0, 2);
// 対照群のイベント率の事前分布(ベータ分布を使用)
for (i in 1:N) {
p_c[i] ~ beta(1, 1); // 一様な事前分布
logRR[i] ~ normal(mu, sigma);
rc[i] ~ binomial(nc[i], p_c[i]); // 修正
rt[i] ~ binomial(nt[i], fmin(p_c[i] * exp(logRR[i]), 1)); // 最大値を1に制限
}
}"
N <- meta_data$N
init_values <- function() {
list(mu = 0, sigma = 1, logRR = rep(0, N), p_c = rep(0.1, N)) # 確率の初期値を設定
}
# Stanモデルのコンパイルと実行
fit <- stan(model_code = stan_model_code, data = meta_data, init = init_values, iter = 2000, chains = 4)
# 推定結果の抽出
posterior_samples <- extract(fit)
mu_samples <- posterior_samples$mu
# リスク比 (exp(mu)) と 95% 信頼区間の計算
risk_ratio <- exp(mean(mu_samples))
conf_int <- exp(quantile(mu_samples, probs = c(0.025, 0.975)))
# 結果の表示
cat("推定されたリスク比:", risk_ratio, "\n")
cat("95% 信頼区間:", conf_int[1], "-", conf_int[2], "\n")
主な修正点:
- モデルを Random effects model に変更
logRR[i] ~ normal(mu, sigma);を維持し、研究間のばらつきを考慮しました。
- スペルミスの修正
binoial distributions→binomial distributionsに修正しました。
- コードの重複部分を削除
rt[i] ~ binomial(nt[i], p_c[i] * exp(logRR[i]));の不要な部分を削除しました。
これで、修正点を反映した適切な Random effects model になっています!
もし追加の調整が必要でしたら、お気軽にご相談ください。
それでは提案されたスクリプトをRで実行してみます。
そして、得られた結果は以下の通りです。
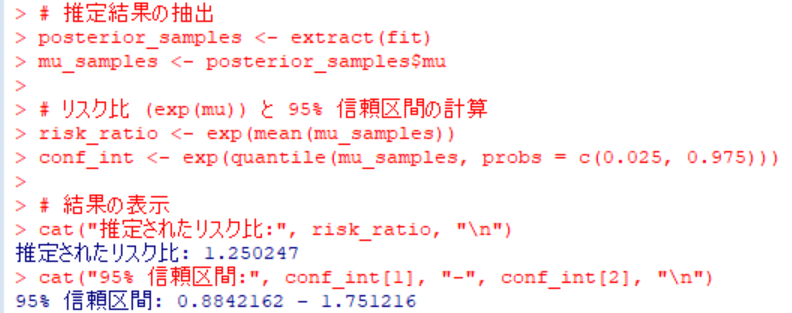
今回のリスク比の統合値は間違いないように見えます。
ただし、# Stanモデルのコンパイルと実行、つまりstan()関数でMCMCを実行した後にサンプリングの数が少ないため平均値や中央値は信頼できませんという警告メッセージが出ていました。

4000のサンプリングでは少ないことは明らかなので、もっと多くしたいと思います。上記のコードではiter 2000, chains 4なのですが、これを大きくすることで対処できるはずです。Warmupの回数も指定したいので、その方法をCopilotに聞いてみましょう。
stan()関数でwarmupの設定はどのようにしますか?
stan() 関数では、warmup の設定を iter と組み合わせて指定します。warmup はMCMCサンプリングの最初の部分で、チェーンの初期化が終わった後に適切なサンプリング状態に到達するまでの試行です。通常、warmup 期間のサンプルは解析には使用されず、モデルの収束を助けるためにのみ使われます。
warmup の設定方法:
fit <- stan(
model_code = stan_model_code,
data = meta_data,
init = init_values,
iter = 2000, # 総サンプリング回数
warmup = 500, # ウォームアップ期間(初期の500サンプルを破棄)
chains = 4 # チェーン数
)
この例では iter = 2000 で全体のサンプリングを行い、最初の 500 サンプル (warmup = 500) はウォームアップとして扱われます。通常、warmup の値は 全体の iter の 25~50% 程度に設定するのが推奨 されています。
注意点:
warmupを適切に設定することで、収束の質が向上します。warmupが短すぎると、収束が不安定になり、バイアスのある推定になる可能性があります。warmupが長すぎると計算コストが増えますが、適切な値を設定することでパフォーマンスを最適化できます。
最適な warmup の値はモデルによって変わるので、トレースプロット (traceplot(fit)) などを確認して、適切な長さを選ぶのがよいでしょう。
試してみて、もしモデルが収束しない場合は warmup の値を調整しながら最適化するのがオススメです。何か他に調整したい点があれば聞いてください!
Warmupは全体のサンプリング回数の25~50%にすることが推奨されているということなので、iter = 40000, warmup =20000, chains =5で100000個のサンプルを得るようにしてみたいと思います。stan()関数の部分を以下の様に書き換え、 もう一度このスクリプトを実行します。
fit <- stan(model_code = stan_model_code, data = meta_data, init = init_values, iter = 40000, warmup = 20000, chains = 5)今度はBulk Effective Samples Size (ESS) is too low, indicating posterior means and medians may be unreliable.という警告は出ませんでした。
その結果です。

############################################
おそらくこれであっていると思われますが、頻度論派のメタアナリシスをRのmetaパッケージで実行してみました。結果を比較してみたいと思います。

リスク比の統合値はほぼ同じで、小数点以下1桁まで、1.2で同じですがそれ以下の桁は異なります。95%信頼区間の値は、Stanのベイジアンアプローチの方は0.8854134~1.744159、metaの頻度論派アプローチの方は1.0196~1.6540で前者の方が幅が広めです。Rのパッケージmetaforでもやってみましたが、metaと全く同じ値が得られました。いずれも研究間の分散の計算にはREML (restricted maximum likelihood)法が使われています。
さて、MCMCをstan()関数で実行した結果が変数fitに格納されており、そこからexract(fit)で取り出された値は変数posterior_samplesに格納されています。その構造を調べるため、str(posterior_samples)を実行すると、以下の結果でした。
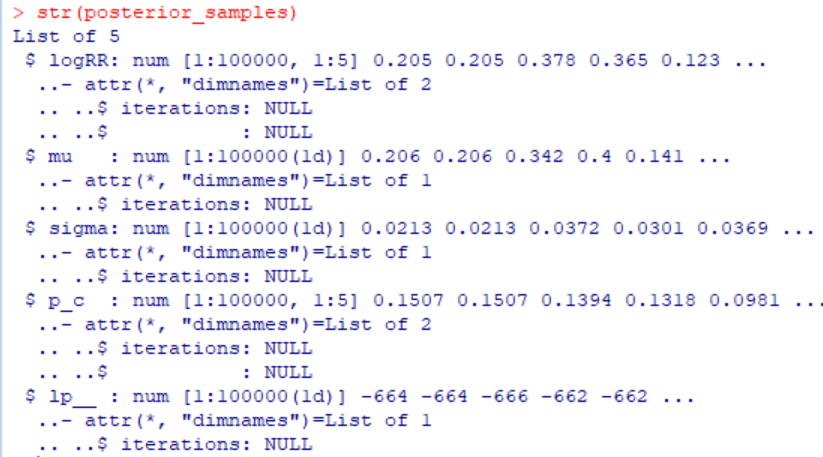
変数logRR, mu, sigma, p_c, lp_が100000個記録されていることが分かります。
ここにlp_という変数が出てきたのでこれが何か聞いてみましょう。
posterior_samplesのlp_は何ですか?
posterior_samples$lp_ は、Stanの出力に含まれる**対数事後確率(log posterior probability)**の値を指します。
StanのMCMCサンプリングでは、各サンプリングステップで**モデルの対数確率(log probability)**を計算しており、それが lp_ という変数として出力されます。
lp_ の意味:
lp_は、MCMCサンプルごとの**対数確率密度(log probability density)**を表します。lp_の値がより高いほど、そのサンプルはモデルにとって「より適合した状態」を示します。traceplot(fit, pars = "lp_")を使うことで、lp_の挙動をプロットし、モデルの収束を確認することができます。
lp_ の使い方:
- 収束診断
lp_の値が一定の範囲で安定しているかどうかを確認することで、MCMCのチェーンが適切に収束しているか判断できます。 - モデル比較
異なるモデルを比較する際に、lp_の平均を確認することで、どのモデルの適合度が高いか評価できます。 - 異常値の検出
lp_の値が極端に低いサンプルは、モデルの異常な状態を示している可能性があるため、適切にフィルタリングすることが重要です。
Stanの出力で lp_ の変動が大きすぎる場合は、モデルの収束が不安定な可能性があるので、ウォームアップの長さ (warmup) や事前分布を調整すると良いでしょう。
もし詳細な活用方法について知りたければ、気軽に聞いてください!
StanのMCMCサンプリングでは、各サンプリングステップで**モデルの対数確率(log probability)**を計算しており、それが lp_ という変数として出力されますとのことでした。収束診断、モデル比較、異常値の検出に使われるとのことです。
##############
今回もCopilotの回答は間違いを含んでいました。Stanをrstanで動作させるには、Rtoolsのインストールが必要なのにそれに言及しなかった、modelはテキストとして変数に格納する必要があることが無視されていた、効果指標として、リスク比を指定したにもかかわらず、オッズ比の例を提案してきた、対照群のイベント率を固定するなどの問題が起きました。しかし、このような間違いや問題はほとんどの場合、実際にRでスクリプトを実行するとエラーが起きるので、それに基づいて修正を提案させることができることも分かりました。Stan, rstanは、今回初めて使用したこと、Stan、rstanのマニュアルや関連した情報を読み込まなくてもできたことを考えると、やはり非常に効率的だと思いました。
Copilotと何回かやりとりしているうちに、Stanのコードの記述法が何となくわかってきました。以下にまとめておきます。
- dataブロックでは、解析対象のデータの変数の属性を設定する。
- transformed dataブロックでは、各変数間の演算を設定する。
- parametersブロックでは平均値などの知りたい値の変数の属性を設定する。
- modelブロックでは、パラメータの事前分布の設定と、パラメータのサンプリングを設定する。
- MCMCの実行はstan()関数で行い、モデル、データ、サンプリング回数とチェーン回数を指定する。(この実行には少し時間がかかる)。
- 結果はstan()関数の実行結果を格納した変数からextract()関数で例えば、posterior_samplesのような変数に取り出し、さらにパラメータの変数名を$で結合して個別に取り出す。
- 個別のパラメータのサンプリングに対して、Rの関数を用いて必要な統計値を得る。
R, Stan, brmsを使ったメタアナリシスに関して、以下のサイトから情報が得られます。今回はCopilotに聞きながらどこまでできるかというのがテーマなので、これらは参照しないでやりました:
Stan Development TeamのStan: Software for Bayesian Data AnalysisおよびRSstan: the R interface to Stan
Matti Vuorre氏のMatti’s homepage Bayesian Meta-Analysis with R, Stan, and brms: Meta-analysis is a special case of Bayesian multilevel modeling
それでも何とかベイジアンアプローチのメタアナリシスが実行できました。結果の妥当性についてのチェックは他のデータでも試す必要がありますし、結果をフォレストプロットにしたり、出版バイアスのチェックはどうやるか、など課題は残っています。また、オッズ比、リスク差、平均値差、標準化平均値差の場合やネットワークメタアナリシスへの拡張なども課題です。
追記:
Warn DEらの論文で記述されているランダム効果モデルによるメタアナリシスのためのWinBUGS用のコードを用い、同じサンプルデータでOpenBUGSで分析を実行したところ、RRの統合値は以下のようにStanの場合と近似した値でした。
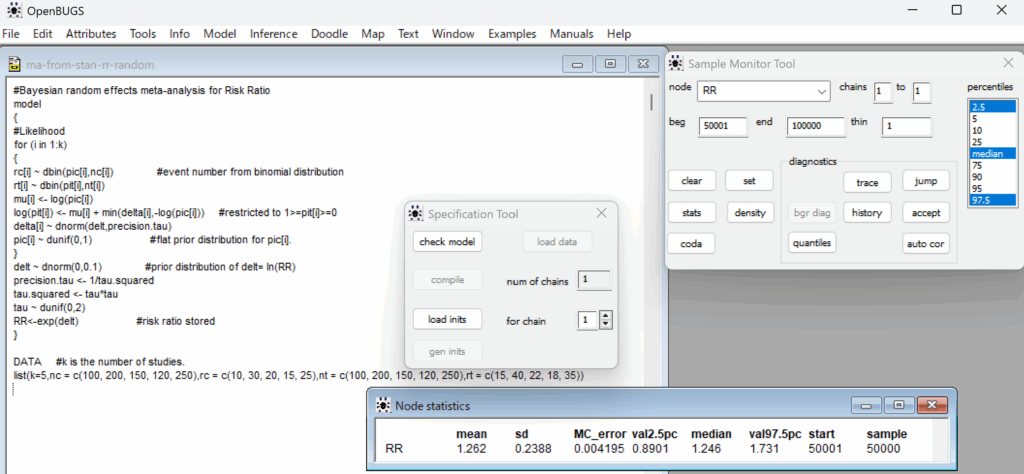
リスク比の統合値は1.246 (95% CI 0.8901~1.731)で上記の結果に近似していました。こちらのモデルはやはり二項分布を用いており、今回のStanのモデルと同じと言えると思います。
BUGSコードの書き方はStanの場合と同じではありません。BUGSでは正規分布の指定に平均値と精度(分散の逆数)を使いますが、Stanは平均値と標準偏差を使います。それ以外にデータ処理については、例えば、RRをlogRRに相当する変数deltをサンプリングする時点で計算し、RRのサンプリングも記録しています。Stanのモデルの方ではRRはサンプリングはしないで、logRRのサンプルから後で計算しています。しかし、rc、rtを二項分布からサンプリングしていることは共通です。
BUGSのコードをStan用に書き換えるのも今後の課題です。もしCopilotやGeminiが正しく変換してくれると楽で良いのですが。
Warn DE, Thompson SG, Spiegelhalter DJ: Bayesian random effects meta-analysis of trials with binary outcomes: methods for the absolute risk difference and relative risk scales. Stat Med 2002;21:1601-23. doi: 10.1002/sim.1189 PMID: 12111922

