ネットワークメタアナリシスって複雑そうですね。
比較する介入が3つ以上はあるからね。原理はペア比較のメタアナリシスと同じなんだけど。
BUGSを使う場合が多いみたいだし、それも難しそうな感じ。BUGSってBayesian inference using Gibbs Samplingのことでしょ。OpenBUGSを使うっていうところでハードルが高いかな。まずは、OpenBUGSって何か知りたいな。
だいたいベイジアンて何だかわからないかもしれないね。でもOpenBUGSを動かして解析結果を得るところまではだれでもできるはず。Network Meta-analysisにはOpenBGUSを使うのが一般的だし、コードもいっぱい発表されているから、全部自分で書かなくてもそれを使って解析ができるようになっている。だから使えるようになりたいですよね。
まずはPCでランダムサンプリングができるということがわかる必要があるんだ。それが確率的シミュレーションの基だし、ベイズ推定Bayesian inferenceで用いるMarkov Chain Monte Carlo (MCMC) simulationの要だから。それをOpenBGUSで実行しながら、OpenBUGSの使い方を見てみよう。
たとえば、BUGSのコード、つまりプログラムで
mu~dnorm(0,0.0001)
って書いてある意味わかる？
dはdistributionで分布という意味でしょう。normは正規分布normal distributionのことでしょう。dnorm()は()がついているので、関数という意味で。。。0が平均値、0.0001は標準偏差か分散か、たしかBUGSでは分散の逆数つまり精度で指定するはず。だから、平均値0、精度0.0001つまり分散なら10,000、標準偏差なら100の正規分布からランダムサンプルを1個得て、変数muに格納するという意味ですよね。
そうそう、その通り。関数なんてよく知ってるね。0と0.0001は関数に与える引数（ひきすう）だよね。
そうですね。もしこのコードを繰り返し実行するとmuは0付近の値が一番多くなるけど、標準偏差が100だから、かなり範囲の広い値が得られますね。そうでしょう。
OpenBUGSをインストールして実際に動かしてみよう。Front pageからサイドバーのDownloadsを開いてダウンロードし、インストールする。通常のWindows用のソフトウェアと同じ。
インストールしてOpenBUGSを起動して、FileメニューからNewを選ぶとEditor画面が出てきますね。
そうそう。そこにこう書き込んでみて。
#Random sampling
model{
mu~dnorm(0,0.0001)
}
こんな風にmodel{ }の{ }の中に動かすコードを書き込みます。今回はしないけど、データや初期値はその外側に書きます。コメントは#に続けて書きます。
Attributesメニューからフォントを12 Pointにして、字を大きく表示するようにしてから、書き込みました。
そうこれでいいね。
このコードを動かす手順を説明するね。まず、ModelメニューからSpecification…を選びます。そうするとSpecification Toolの画面が出てきます。そしたら、コードのmodelの文字列をダブルクリックして選択した状態にします。やってみて。
こうですね。
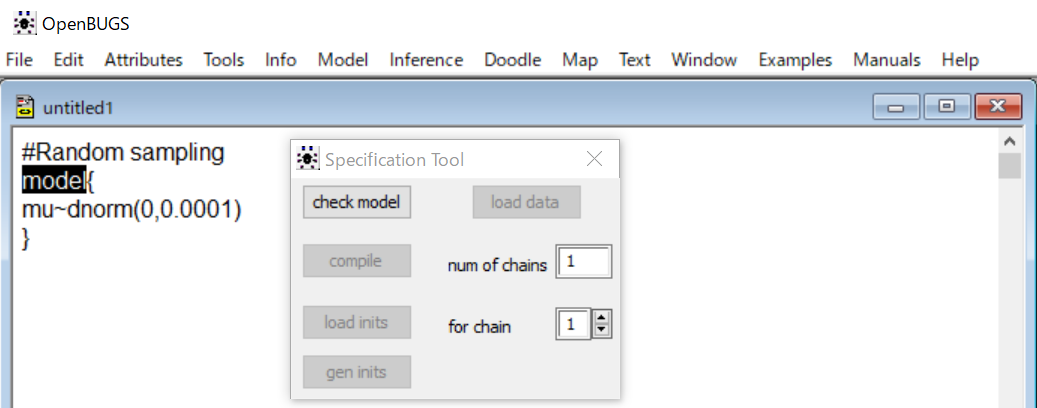
そうそう。そしたら、check modelボタンをクリックしてこのコードを読み込ませるとともにプログラムの整合性をチェックさせます。問題なければ、Editor画面の下の枠にmodel syntactically correctとメッセージが表示されます。
あ、出ました。load dataとcompileのボタンがアクティブになりましたよ。
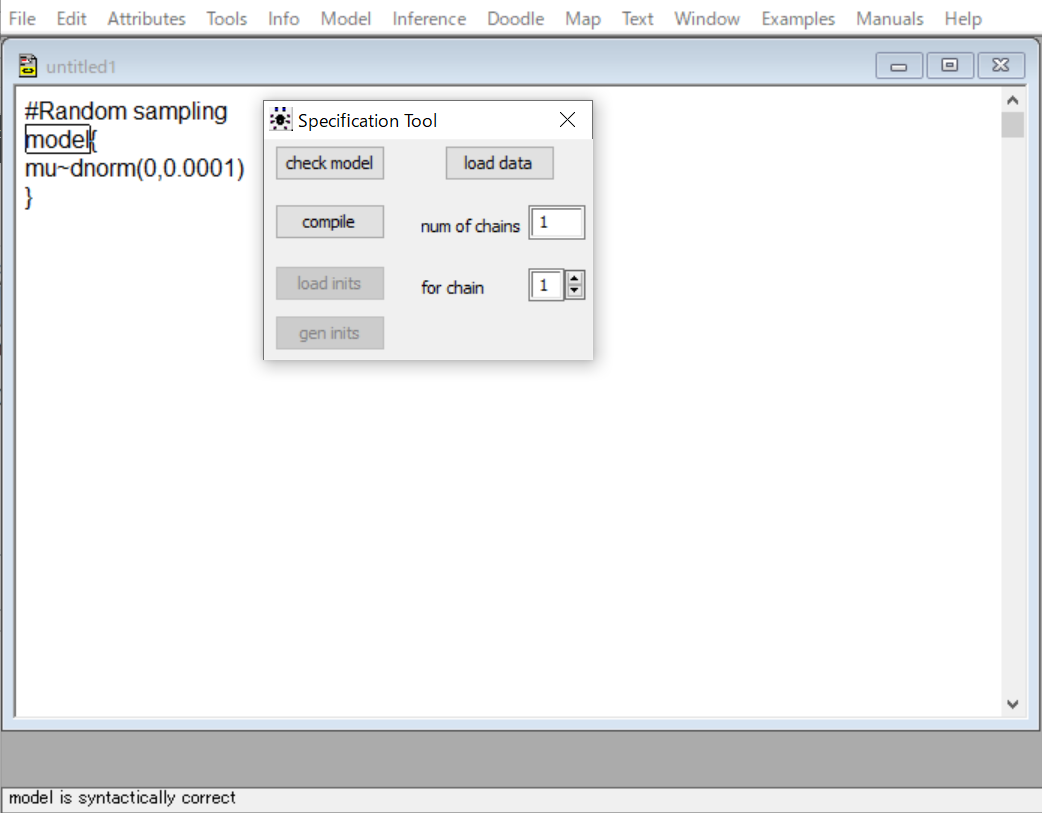
そうそう。今回はデータの読み込みは必要ないので、load dataは飛ばして、compileボタンをクリックします。
compileボタンをクリックしたら、下にmodel compiledと出ました。load initsとgen initsのボタンがアクティブになりましたね。initsって初期値の設定のことですか？
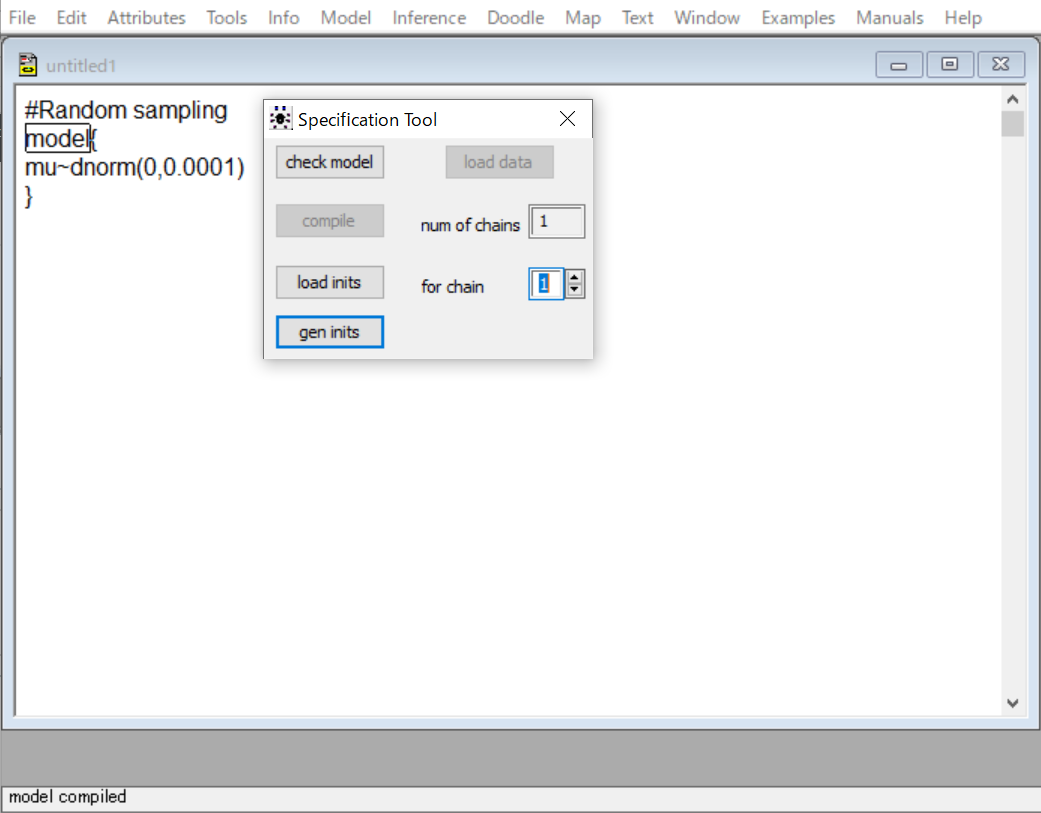
そうなんだ。Markov Chain Monte Carlo (MCMC) simulationをするときに最初の値を設定する必要があるんです。OpenBUGSは、普通はGibbs samplerを用いてMCMC simulationを実行するために作られているので、初期値の設定をしないと次に進めないようになっているんだ。
このEditor画面のmodel{ }の下に書き込んでおいて、それをload initsで読み込ませて設定することもできるんだけど、今回はdnorm(0,0.0001)を一回実行させて得られた値を用いることにして、gen initsボタンをクリックしましょう。gen initsはgenerate initial valuesという意味ですね。
はーい、やってみました。下の方に、initial values generated model initializedと出ました。これで、コード実行の準備ができたみたいですね。
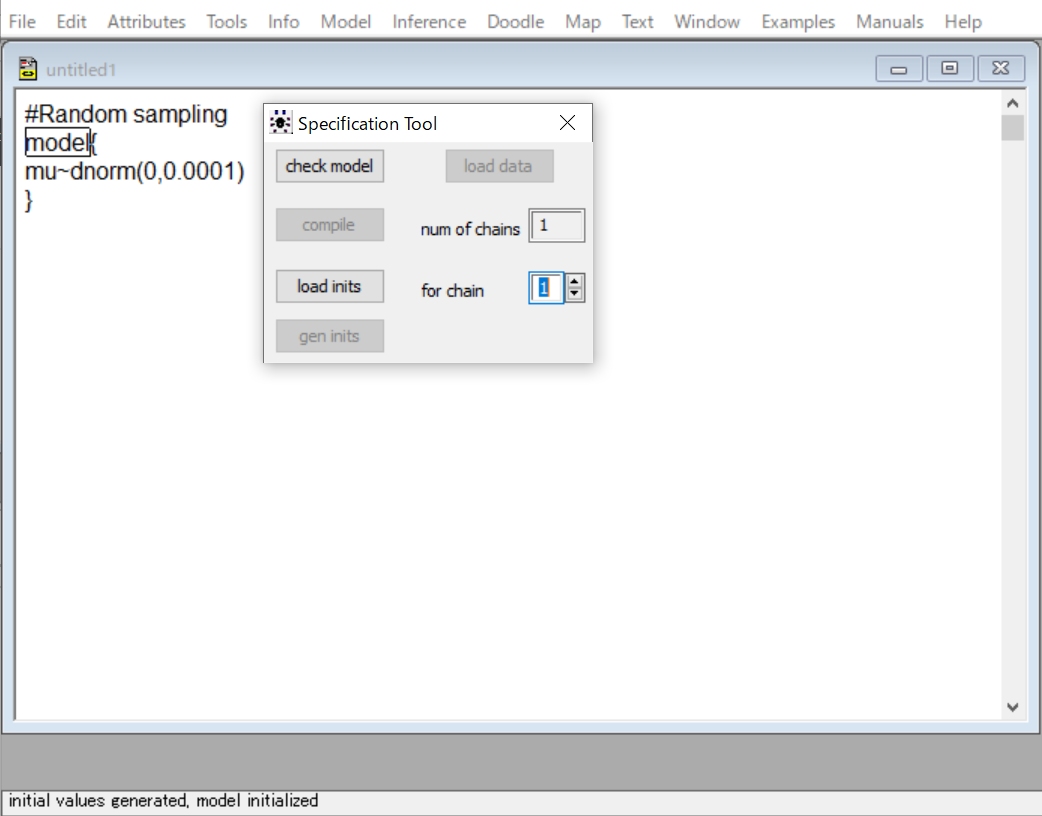
その通り。それでは、muの値を記録するために、InferenceメニューからSamples…を選んで、Sample Monitor Toolの画面を出しましょう。
はい。こうですね。nodeって書いてありますね。OpenBUGSではvariableじゃなくて、nodeという言い方をするんですね。
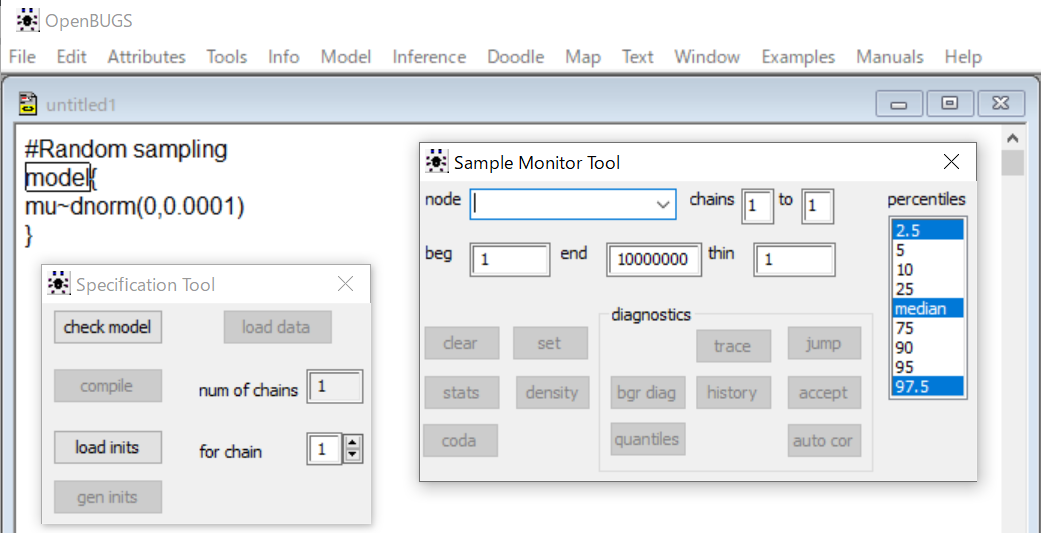
そう、そこに記録したい変数の名前を入力してsetボタンをクリックします。今回は、muひとつしかないので、muと入力すると、setボタンがアクティブになるので、そのボタンをクリックするだけです。
普通は、もっとたくさん記録したい変数があるので、コードを眺めながら、設定作業を繰り返すことになります。
記録するという意味は、ランダムサンプリングした値を後で出てくるupdateの数だけ、全部記録するという意味です。その値から、平均値を計算したり、分布を見たりすることになります。
普通のMCMCの場合は、このnodeの設定をする前に、Burn-inという、記録しないで、MCMCを実行させ、平衡状態に達した後にnodeを設定します。今回は、そのステップは飛ばして、最初から記録させます。
はい、muと入力してsetしました。setボタンをクリックするとnodeのフィールドが空になって、下のボタンが全部すぐinactiveになりますね。
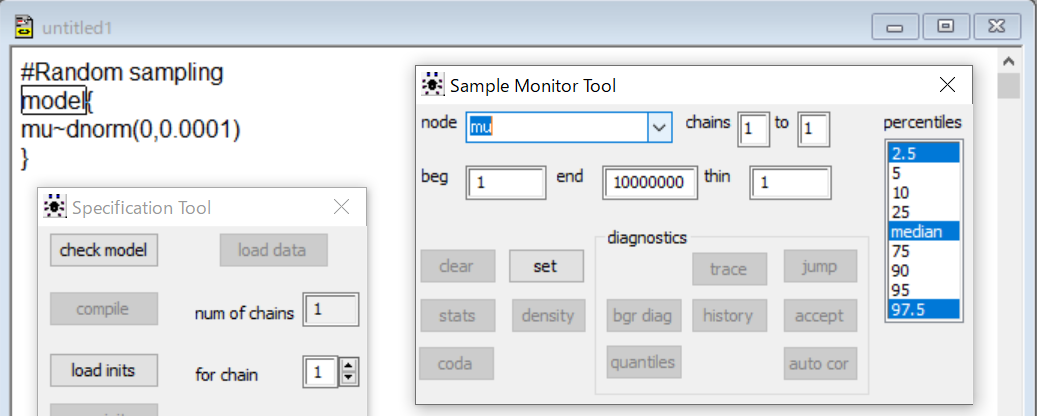
そうそう。連続してnodeの設定することがやりやすいようになっているんだね。設定したnode (変数名）はnodeのフィールドの右にあるプルダウンメニューを開くと確認できます。
今度は、いよいよランダムサンプリングを実行するんだけれど、ModelメニューからUpdate…を選んで、Update Toolの画面を出してみて。そのupdatesというところに、ランダムサンプリングを何回実行するか、つまり何個ランダムサンプルを得るかを設定するんだ。
こうですね。デフォルトではupdatesが1000になってますね。今回は、10000にしてやってみましょうか。
多くの場合、1万から5万回の設定で十分みたいですね。多くすると処理に時間がかかります。モデルが複雑で、nodeの数が多いと何分もかかることはよくあることです。
updates 10000でupdateボタンをクリックして実行しました。あっという間に終了しました。下の方に、6秒かかったと出てます。これで、平均値0、標準偏差100の正規分布から、1万個のランダムサンプルが得られ、変数muに格納されたということですね。
そうですね。実際にランダムサンプリングされた値を見てみましょう。その後に、分布、平均値、中央値、95%確信区間などのデータを見ることにしましょう。
Sample Monitor Tool画面で、nodeのプルダウンメニューを開いて、muを選択してみてください。muと入力してもいいです。
nodeの下のボタンがアクティブになりましたね。statsとdensityとcodaのボタンもアクティブになりました。
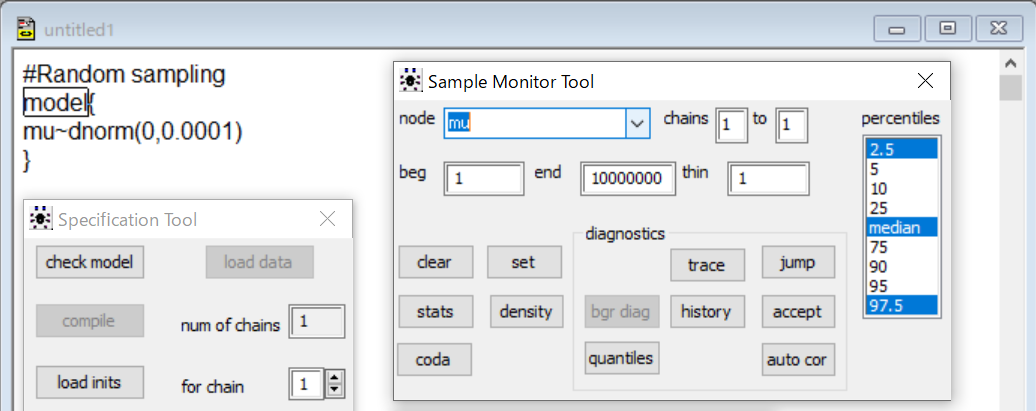
そこで、codaのボタンをクリックするとランダムサンプリングされた値が表示されます。ランダムサンプリングってどういうことなのか分かると思うので、見てみましょう。
なんか二つ出てきました。ウインドウが重なるので、その部分だけ出すとこんな感じです。CODA indexとCODAchain 1っていう名前がついてますね。
CODAchain 1に表示されている値を見ると、バラバラですね。本当にランダムな感じですね。平均値0の正規分布だから、0前後の値が多いはずですよね。
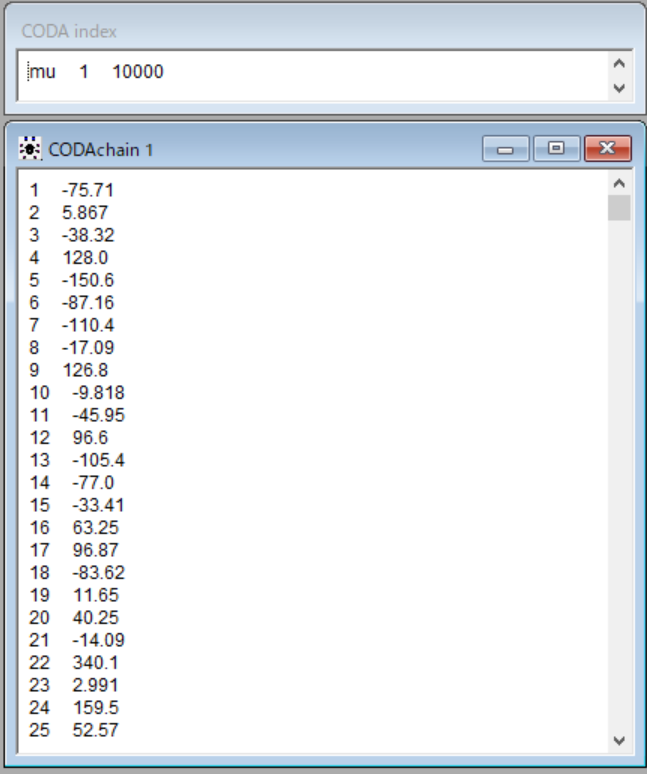
CODAってConvergence Diagnostic and Output Analysisのことらしいんだけど、Rのパッケージでcoda: Output Analysis and Diagnostics for MCMCというのがあって、それを使って、このデータを解析することもできるんです。
今回は変数一つだけなので、CODA indexにはmuという変数は1行目から10000行目までの値だということしか書かれていないですね。別の例を見せるけど、それぞれの変数のサンプリングされた値がどの行からどの行までかという情報が含まれています。
C_new 1 20000
C_overall 20001 40000
LAMBDA 40001 60000
S_new 60001 80000
S_overall 80001 100000
THETA 100001 120000
CODA indexもCODAchain 1もそのウインドウを選択して、FileメニューからSave As…でファイルの種類をPlain text(*.txt)にしてテキストファイルとして保存し、あとで利用することもできます。Rからread.table( )で読み込んで解析もできます。CODA indexはdataframeとして行と列の位置を指定して CODAchainの方は数値型のvectorとして、何番目か位置を指定して値を読み出すことができるんだ。
Rはオープンソースウェアで統計解析に広く用いられているのは知ってるよね。もしRで同じことをするなら、mu=rnorm(10000,0,100)を実行するだけで、一瞬で1万個のランダムサンプルが得られるんだけど、今はOpenBUGSの勉強。
さてそれでは、分布をみてみましょうね。densityボタンをクリックしたらグラフが出てきました。statsボタンもクリックしてみました。
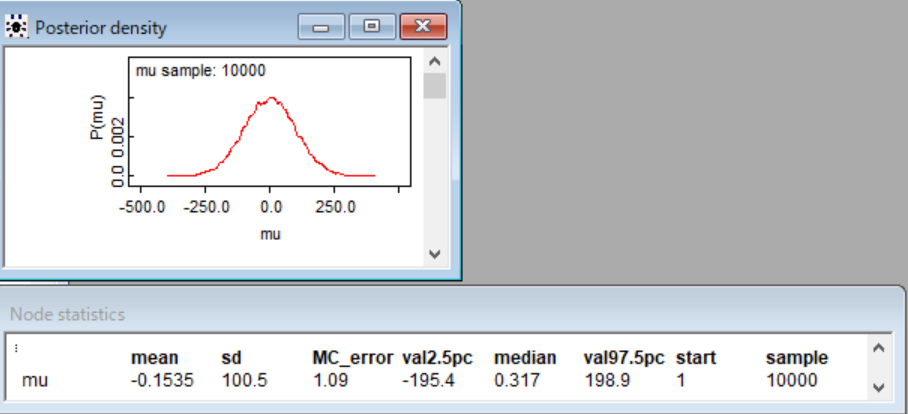
グラフを見ると平均値0で標準偏差100の正規分布だとわかりますね。Node statisticsの実際の値を見るとわずかな誤差はあるけど、meanはほぼ0、sdはほぼ100になってますね。updatesをもっと増やすと、さらに正確な値になるでしょう。この分布を代表する値が得られていることが実感できるね。
おもしろいですね。平均値と標準偏差の値を設定するとその正規分布からランダムサンプルを得るシミュレーションが簡単にできるんですね。
さてそれじゃ、load dataとload initsも試してみようか。load dataで平均値と標準偏差の値を設定して、精度は標準偏差の二乗分の1を計算させて、muの初期値は0に設定して、updatesは50000にしてやってみよう。
解析に必要な3つのウインドウは同時に表示できるので、今度はModelメニューからSpecification…、InferenceメニューからSamples…、さらにModelメニューからUpdate…を選んで、Specification Tool、Sample Monitor Tool、Update Toolの3つのウインドウを表示させてから以下の操作をやってみよう。
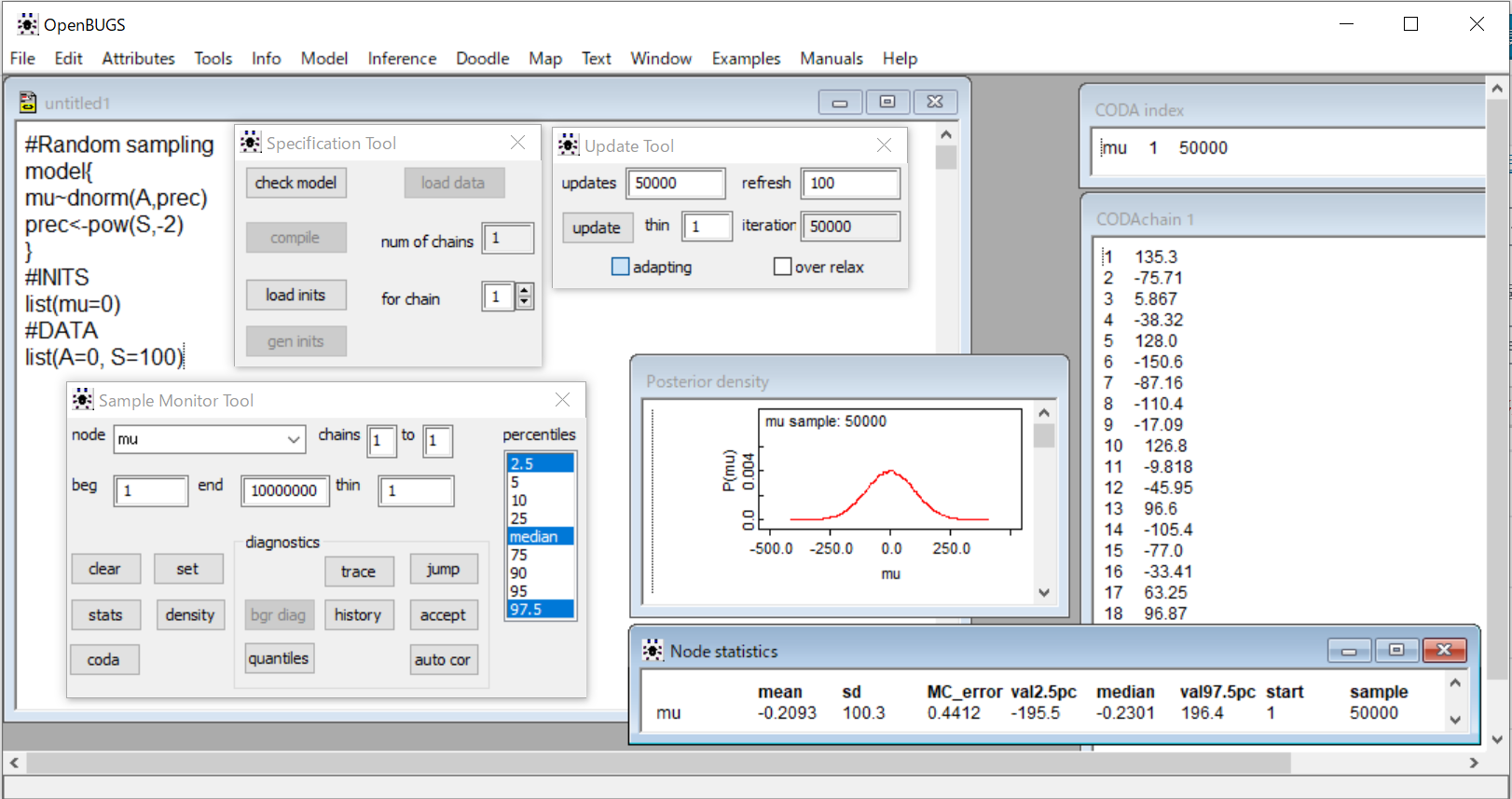
操作の順序は同じですね。順番に、
1. コードのmodel部分をダブルクリックして選択したらcheck modelのボタンをクリックし、
2. 次に#DATAのlistという部分をダブルクリックして選択してから、load dataボタンをクリックする。
3. 次に、compileボタンをクリックして、
4. 今度は#INITSのlistという部分をダブルクリックして選択してから、load initsボタンをクリックする。
5. 次に、Sample Monitor Toolでnodeにmuと入力して、setボタンをクリックする。
6. Update Toolでupdatesを今度は50000にして、
7. updateボタンをクリックする。ここで少し時間がかかる。
8. シミュレーションが終了したら、Sample Monitor Toolでnodeにmuと入力して、density, stats, codaのボタンをクリックして、結果を見る。
そうそう。コードはこんな風になっているんだ。
#Random sampling
model{
mu~dnorm(A,prec)
prec<-pow(S,-2)
}
#INITS
list(mu=0)
#DATA
list(A=0, S=100)
このコードはEditor画面を選択して、FileメニューからSave…あるいはSave As…でOpenBUGSの形式であるodcあるいはテキストファイル形式で保存できます。
なるほど、31秒で終了しましたね。結果はほとんど同じですね。でも分布の曲線がなめらかになっている。
コードを見ると、標準偏差Sの2乗分の1を計算して、つまり分散の逆数を計算して、precという変数に代入するコードが追加されていて、<-って書かれていますね。muのところも、dnorm( )に平均値はA、精度はprecが引数として設定されてますね。~はランダムサンプルを代入、<-はその値を代入するんですね。
SとAの値は、データとしてlist形式で与えられているんですね。標準偏差の方がわかりやすいからこっちの方がいいですね。
list部分をダブルクリックして選択してからload dataボタンをクリックすると値が設定されるわけですね。listの中はコンマで区切って複数の変数の設定ができるんですね。それと=で代入が行われるんですね。コードの中では、<-を使うのと違います。
muの初期値も同じように設定したということですね。
なんかすごいですね。OpenBGUSの操作が少し分かってきたので、次は、Network Meta-analysisをやってみたいです。
続きはこちら。