Diagnostic Test Accuracy (DTA) 診断精度研究のMeta-analysis (MA)メタアナリシスは介入の効果のメタアナリシスとは異なります。手法が異なるだけでなく、結果の解釈や活用法も異なります。
DTA MAの結果、感度・特異度の統合値と95%信頼区間、陽性尤度比、陰性尤度比、診断オッズ比(Diagnostic Odds Ratio, DOR)、Summary Receiver Operating Characteristic (SROC) curve、およびSROCの曲線下面積(Area under the curve, AUC)などの推定値が得られます。
DTA MAの統計学的モデルとして、Reitsma のBivariate model二変量モデル、階層モデルである Rutter & GatsonisのHierarchical Summary Receiver Operating Characteristic (HSROC)モデルの使用が推奨されています。共変量を用いない場合は二変量モデルとHSROCモデルは数学的に同じものです(Arends LR;Harbord RM) 。
DTA MAに関する書籍としては、Biondi-Zoccai G ed. Diagnostic Meta-Analysis: A Useful Tool for Clinical Decision-Making. Springer, Cham, Switzerlandが包括的な内容で、有用と思います。また、Cochrane Handbook for Systematic Reviews of Diagnostic Test Accuracyは2022年度Version 2が発表されており、包括的な内容で、SAS、R用のスクリプトが具体的に解説されており、有用だと思います。
Reitsma JBのオリジナルの論文では、近似正規分布を用いるため、症例数が少なく、感度・特異度が95%程度に高い場合には、誤差が大きくなることをChu Hらが指摘しており、Cochraneはコクランのシステマティックレビューに使用することは推奨しないとしています。また、ゼロイベントのある場合に0.5を加算して補正する方法もずれを生じます。そのため、広く使用されているRのパッケージであるmadaの使用は推奨できないと述べられています。実際に、Chu Hらの論文でシミュレーションの結果を見ると、症例数が25例以下、感度・特異度が95%以上になると二項分布を用いる場合とずれが大きくなるのは確かですが、Chu HのLetterに対するReitsma JBの返答で述べられているように、多くの場合臨床上の問題を生じるほどではないと考えられます。
Cochrane Handbook for Systematic Reviews of Diagnostic Test AccuracyのAppendix 14では同じ対象者でCTとMRIを施行し、診断能を比較した5つの研究のDTA MAの例が記載されており、Rのlme4パッケージのglmer()関数を用いて、GLMM (Generalized Linear Mixed Effects Model)で二項分布による回帰モデルを用いています。Appendix 12では同じ対象者で二つの診断法を実施したのではなく、別の対象者でそれぞれの診断法の感度・特異度を測定した研究をもとに、二つの診断法の診断能を比較するための解析法が記載されています。こちらは、間接的な比較という表現が使われており、同じ対象者で直接比較した研究も含めて解析できる方法が示されています。
感度のロジットと偽陽性率のロジットを従属変数とし、各研究の感度のロジットと偽陽性率ロジットで回帰モデルを作っています。ロジットはオッズの自然対数、つまりlogit(se)=ln[se/(1-se)], logit(sp)=ln[sp/(1-sp)], logit(fpr)=-logit(sp)です。
具体的には図1に示すようなデータに対して、回帰分析を行い、ロジットのExponentialでオッズに変換し、さらにオッズ/(1+オッズ)で割合に変換して感度・特異度の値を求めています。図1の例は同一症例でCTとMRIを施行しており、これら二つの検査法の感度・特異度の統計学的な比較が行われています。
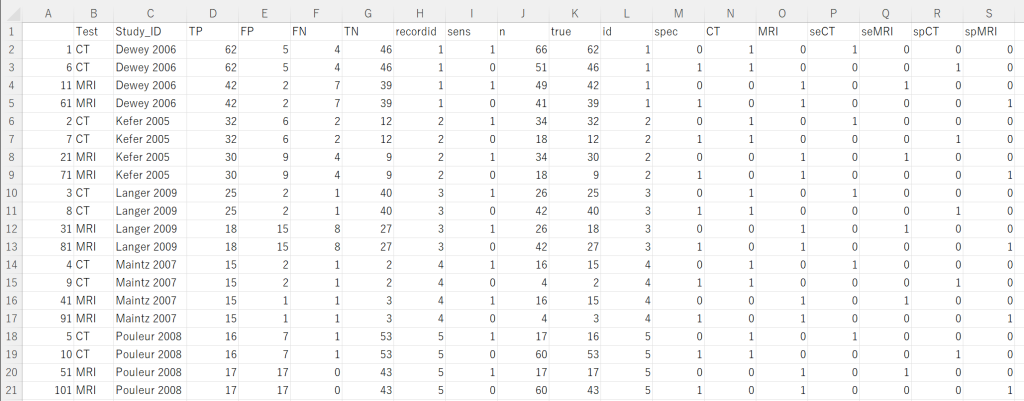
通常、元になるデータは各研究IDとTP, FP, FN, TN (True Positive, False Positive, False Negative, True Negative)の人数のデータと検査法のデータです。それらから、図1の形式のデータフレームを作成し、以下のスクリプトで解析を行います。
###Comparison of sensitivity and specificity between two tests done in the same subjects###
###Random-effects meta-analysis with bivariate model using binomial distribution###
library(lme4)
library(lmtest)
###Y is a data frame as shown in Fig. 1###
(B = glmer(formula=cbind(true, n – true) ~ 0 + seCT + seMRI + spCT + spMRI + (0+sens + spec|Study_ID), data=Y, family=binomial))
(C = glmer(formula=cbind(true, n – true) ~ 0 + sens + spCT + spMRI + (0+sens + spec|Study_ID), data=Y, family=binomial))
###Is there a statistically significant difference in sensitivity between CT and MRI?
lrtest(B,C)
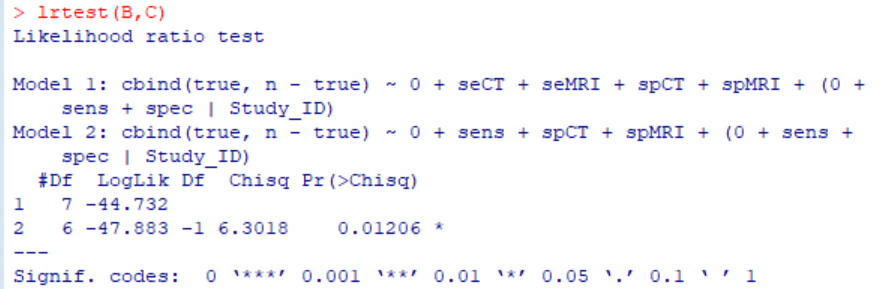
###Is there a statistically significant difference in specificity between CT and MRI?
lrtest(B,D)

実際には各研究IDとTP, FP, FN, TN のデータから図1の形式のデータフレームを作成する部分のスクリプトも必要ですが、ここではlmer()関数の回帰モデルと図1のデータラベルの関係を考えて、回帰分析とメタアナリシスの関係を考えるきっかけになればと思います。
なお、ここでは触れませんでしたが、感度・特異度の統合値と95%信頼区間の計算はCTとMRIについて別々に回帰分析を行った結果から算出します。
文献:
Chu H, Cole SR: Bivariate meta-analysis of sensitivity and specificity with sparse data: a generalized linear mixed model approach. J Clin Epidemiol 2006;59:1331-2 author reply 1332-3. doi: 10.1016/j.jclinepi.2006.06.011 PMID: 17098577
Reitsma JB, Glas AS, Rutjes AW, Scholten RJ, Bossuyt PM, Zwinderman AH: Bivariate analysis of sensitivity and specificity produces informative summary measures in diagnostic reviews. J Clin Epidemiol 2005;58:982-90. doi: 10.1016/j.jclinepi.2005.02.022 PMID: 16168343
Rutter CM, Gatsonis CA: A hierarchical regression approach to meta-analysis of diagnostic test accuracy evaluations. Stat Med 2001;20:2865-84. PMID: 11568945
Harbord RM, Deeks JJ, Egger M, Whiting P, Sterne JA: A unification of models for meta-analysis of diagnostic accuracy studies. Biostatistics 2007;8:239-51. doi: 10.1093/biostatistics/kxl004 PMID: 16698768
Arends LR, Hamza TH, van Houwelingen JC, Heijenbrok-Kal MH, Hunink MG, Stijnen T: Bivariate random effects meta-analysis of ROC curves. Med Decis Making 2008;28:621-38. doi: 10.1177/0272989X08319957 PMID: 18591542

