CochraneのRevMan, Rパッケージのmeta, metaforで用いられているメタアナリシスの手法は伝統的統計学すなわち頻度論派Frequentistの手法です。一方、ネットワークメタアナリシスのためのRパッケージであるgemtcはベイズ統計学に基づく手法を用いるベイジアンメタアナリシスを実行します。Arm-based modelを用いるネットワークメタアナリシスのためのRのパッケージであるpcnetmetaもベイジアンアプローチを用いています。ベイジアンアプローチでペアワイズのメタアナリシスをを行うには、OpenBUGS、JAGS、StanなどMarkov Chain Monte Carlo (MCMC)シミュレーションを実行するためのソフトウェアがRのパッケージであるR2OpenBUGS, rjags, rstanなどを介して用いられています。
頻度論派の手法で得られる統合値と信頼区間Confidence Intervalとベイジアンの手法で得られる統合値と確信区間(信用区間)Credible Intervalは同じように解釈すべきではありません。どのように違うのかを理解するために、以下メタアナリシスではありませんが、2群のイベント数からリスク比と信頼区間あるいは確信区間を計算する実例を示しながら解説したいと思います。
対照群のイベント割合(率)が0.5で介入群のイベント割合(率)が0.4が真のパラメータだとします。真のリスク比の値は0.4/0.5 = 0.8ですが、サンプルから得られる値は、必ずしも0.8にはなりません。例えば、対照群の症例数50例、介入群の症例数50例でランダム化比較試験が行われたとします。各群の50例中イベントが起きる人数は、ランダムサンプルであればこれらの値は二項分布に従い、必ず25人、20人になるというわけではありません。サンプリングの偶然の偏りで少しずつ違う値になります。そして、リスク比も必ず0.8になるわけではありません。これをRでシミュレートしてみます。
対照群の症例数をcsampleSize、イベント率をcprop、介入群の症例数をisampleSize、イベント率をipropで表すと、対照群のイベント数ceventsと介入群のランダムサンプリングで得られるイベント数ieventsをRでは次のスクリプトで得られます。
cevents <- rbinom(1, csampleSize, cprop) # 対照群イベント数 生成回数分
ievents <- rbinom(1, isampleSize, iprop) # 介入群イベント数 生成回数分
これは二項分布からランダムサンプルを得るrbinom()関数を用いていますが次のような考え方に基づいています。ランダム化比較試験の参加者が1名いた場合、その人が介入群に割り付けられると、0.5の確率でイベントが起きる訳ですが、結果として起きるか起きないかは0.5の確率です。次の対照群の参加者1名についても、同じことが言え、0.5の確率でイベントが起きる訳ですが、結果として起きるか起きないかは0.5の確率です。これを50人分繰り返した結果イベントが起きた人数は二項分布に従うので、Rのrbinom()関数では、rbinom(生成回数、ひとつの観測あたりの試行回数,各試行の成功確率)で試行回数でイベントが起きる回数=成功回数が得られます。通常は、同じランダム化比較試験は1回しか行わないので、生成する乱数の個数は1にした場合に相当しますが、この値を変数cycで設定すると、cycで設定した回数分のイベント数のデータが得られます。cycを例えば、100に設定すると、同じランダム化比較試験を100回行った場合の、対照群、介入群のイベント数をシミュレートすることができます。
cyc = 100; csampleSize = 50; cprop = 0.5
isampleSize = 50; iprop = 0.4
cevents <- rbinom(cyc, csampleSize, cprop) # 対照群イベント数 試行回数分
ievents <- rbinom(cyc, isampleSize, iprop) # 介入群イベント数 試行回数分
このスクリプトを実行すると、ceventsには25前後の値が、ieventsには20前後の値がそれぞれ100個格納されます。各群のイベント数からリスク比を計算することができるので、100個のリスク比の値を得ることができます。さらに、それぞれのイベント数と症例数から95%信頼区間を計算することができます。
リスク比の自然対数の95%信頼区間は以下の式で計算されます。すなわち、リスク比の自然対数の標準誤差 = 1/対照群のイベント数 + 1/介入群のイベント数 – 1/対照群の症例数 – 1/介入群のイベント数、をまず計算します。リスク比の自然対数に標準誤差×1.96をプラスマイナスし、計算結果のExponentialを求めると、リスク比の値に戻せます。なお、イベント数が0の場合はゼロの割り算が発生するので、0を0.5に置き換えておきます。
cevents[cevents == 0] = 0.5
ievents[ievents == 0] = 0.5
p_c <- cevents / csampleSize
p_i <- ievents / isampleSize
rr <- p_i / p_c
log_rr <- log(rr)
var_log_rr <- (1 / cevents + 1 / ievents) – (1 / csampleSize + 1 / isampleSize)
se_log_rr <- sqrt(var_log_rr) #Val(logRR)の標準誤差
z <- 1.96
lower_rr <- exp(log_rr – z * se_log_rr)
upper_rr <- exp(log_rr + z * se_log_rr)
グラフ表示までのすべてのスクリプトを以下に示します。変数の値を変えて様々な例をシミュレートすることができます。(スクリプトの一部は行頭に#を置いて実行されないようにコメント扱いにしています。プロット作成にggplot2パッケージを使っています。)
リスク比のシミュレーションのためのRスクリプト
###########################
#リスク比と95%信頼区間のシミュレーション
set.seed(123)
# パラメータ
cyc <- 100 # 生成回数(同じ研究の回数)
csampleSize <- 50 # 対照群 50 人
isampleSize <- 50 # 介入群 50 人
cprop <- 0.5 # 対照群イベント割合
iprop <- 0.4 # 介入群イベント割合
# cyc回だけイベント数を生成 二項分布
cevents <- rbinom(cyc, csampleSize, cprop) # 対照群イベント数 生成回数分
ievents <- rbinom(cyc, isampleSize, iprop) # 介入群イベント数 生成回数分
cat("Control events:", cevents, "of", csampleSize, "\n")
cat("Intervention events:", ievents, "of", isampleSize, "\n")
# RR と 95%CI を計算できるかチェック
#if (cevents == 0 | ievents == 0) {
# stop("どちらかの群でイベント数が0のため、この定義ではRRと95%CIを計算できません。")
#}
# ゼロイベントの場合の処理 0.5に設定する。
cevents[cevents == 0] = 0.5
ievents[ievents == 0] = 0.5
# リスク比
p_c <- cevents / csampleSize
p_i <- ievents / isampleSize
rr <- p_i / p_c
log_rr <- log(rr)
# リスク比の自然対数の分散: Var(logRR) = (1/cevents + 1/ievents - 1/csampleSize - 1/isampleSize)
var_log_rr <- 1 / cevents + 1 / ievents - 1 / csampleSize - 1 / isampleSize
se_log_rr <- sqrt(var_log_rr) #Val(logRR)の標準誤差
# 95%信頼区間(logスケール → 元のスケール)
z <- 1.96
lower_rr <- exp(log_rr - z * se_log_rr)
upper_rr <- exp(log_rr + z * se_log_rr)
cat("RR =", rr, "\n")
cat("95% CI = (", lower_rr, ",", upper_rr, ")\n")
#######
library(ggplot2)
# 理論上のRR
true_rr <- iprop / cprop
# 結果をデータフレーム化
df <- data.frame(
iter = 1:cyc,
rr = rr,
lower = lower_rr,
upper = upper_rr
)
# true_rr が CI の外側にあるかどうかの判定
df$flag <- ifelse(true_rr < df$lower | true_rr > df$upper, "out", "in")
ggplot(df, aes(x = iter, y = rr)) +
geom_point(aes(color = flag), size = 3) +
geom_errorbar(aes(ymin = lower, ymax = upper), width = 0.1) +
geom_hline(yintercept = true_rr, linetype = "dashed", color = "red") +
coord_flip() +
scale_color_manual(values = c("in" = "black", "out" = "red")) +
labs(
x = "Iteration",
y = "Risk Ratio (RR)",
title = "Risk Ratio with 95% CI (points outside true RR highlighted)"
) +
theme_minimal(base_size = 14) +
theme(legend.position = "none")
########
dev.new()
hist(rr, breaks = 30,
main = "100 samples of RR",
xlab = "RR",
col = "lightblue",
border = "white",
freq = FALSE) # 密度スケールにする
# 密度曲線を追加
#lines(density(rr),
# col = "red",
# lwd = 1)
###########################################################上記のスクリプトを実行した結果です。点がリスク比の値で、バーは95%信頼区間を表します。
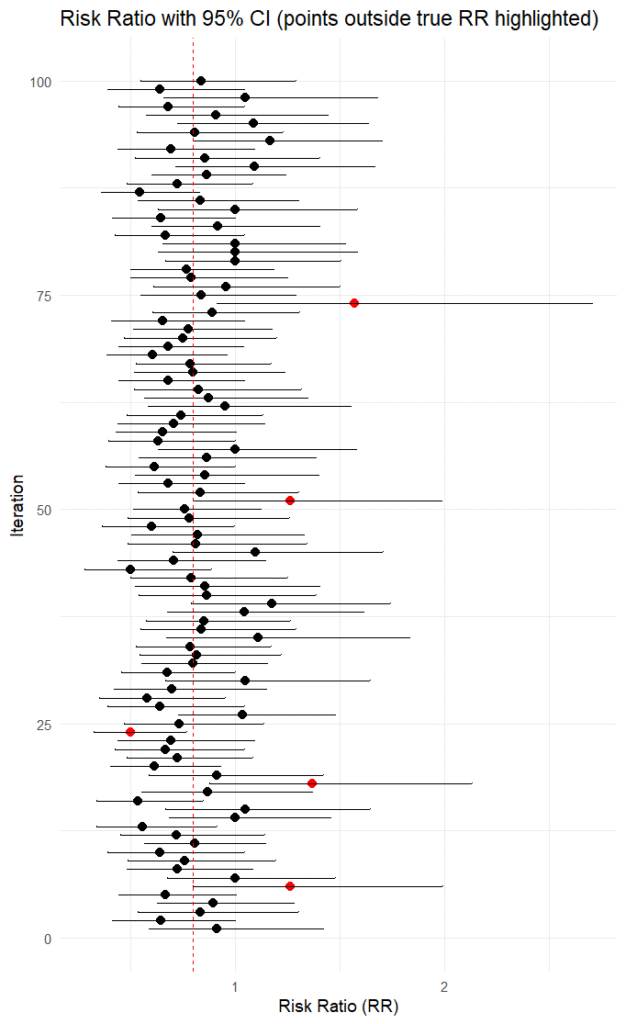
df$rr、df$lower、df$upperには生成回数分のリスク比、95%信頼区間の下限値、上限値、この例では100個の値が格納されていますので、例えば、df$rr[24], df$lower[24], df$upper[24]で24番目のリスク比、95%信頼区間の下限値、上限値の値が得られます。
1回のランダム化比較試験で得られるリスク比の値はこの値の中のどれか一つになります。ただし、もし、選択バイアスその他のバイアスの影響を受けると、リスク比の値は過大評価あるいは過少評価の方向へ少しずれますが、ここではバイアスは無いことを前提とします。ここで、たとえば、赤で示すリスク比の値が得られた場合、その95%信頼区間には真の値である0.8は含まれていません。今回のシミュレーションでは赤で示すリスク比は5個あり、100回中95回はその95%信頼区間に真の値が含まれていました。
頻度論派で得られる95%信頼区間は同じことを100回繰り返したら、95回は真の値を含んでいるという意味です。その時得られた信頼区間には真の値が含まれているか含まれていないかのどちらかです。95%信頼区間があたかも真の値の分布に基づいているという風に解釈するのは間違いです。リスク比の値も毎回異なりますが、信頼区間の値も毎回異なるので、それだけでも95%信頼区間があたかも真の値の分布に基づいているという風に解釈するのは間違いだということが分かります。
頻度論派で得られる95%信頼区間に基づいて、一定の閾値、例えば、リスク比1.0以上の確率を論じることはできません。今回のシミュレーションによる100個のリスク比の例を見てもわかる通り、リスク比1.0以上の確率は毎回異なります。信頼区間は真の値あるいはパラメータの分布に基づいているわけではありません。同じ試行を何回も繰り返し、そのたびに95%信頼区間を計算すると95%の場合は、真の値がその区間に含まれているという意味です。
上記の図を見ると、リスク比の値は真の値である、0.8の近くに多いことが分かります。リスク比の値のヒストグラムは以下の通りです。100個のサンプルですが、生成回数を多くするとより連続的なスムーズな確率密度分布が得られます。
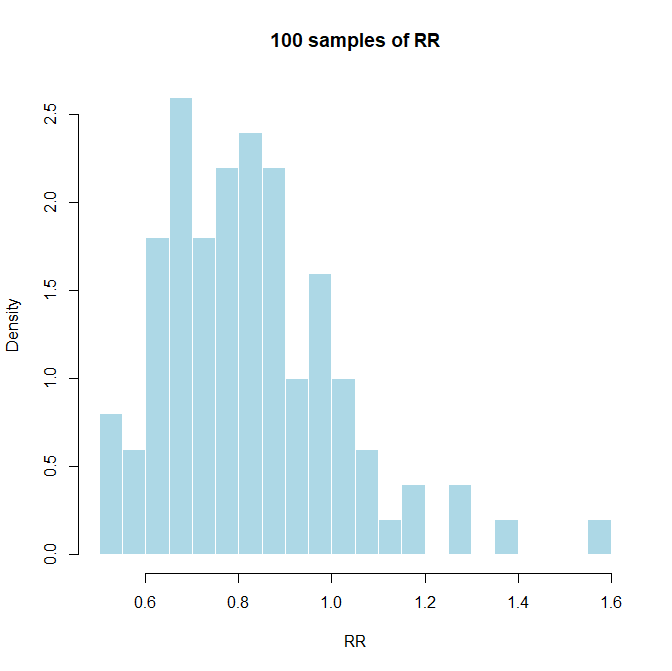
もし、真の値が分かっているのであれば、サンプルサイズとイベント数を指定することで、このような分布を知ることができます。
サンプルサイズが大きくなれば、真の値に近づくことができるということは言えますが、実際には有意であることを証明できるサンプルサイズでの1回の臨床試験の値しか知ることができないので、このようなパラメータの分布を頻度論派のアプローチでは知ることは困難です。
一方、ベイジアンのアプローチでは1回の試行の値を知ることで、それに基づいたパラメータの分布を知ることができます。パラメータは、ここではリスク比の真の値の分布と考えてもいいでしょう。そのパラメータの分布はそのデータに基づいていて、一定の閾値以上あるいは以下の、あるいはある範囲の確率をその時点で議論することが可能になります。もし、同じ研究をもう一度行った場合、それ以前のデータに基づく分布を事前分布として、その新しいデータでアップデートして事後分布を求めることができます。
Stanをrstanから動かして、対照群50例で25例にイベントが起き、介入群50例で20例にイベントが起きたというデータが得られた場合の、リスク比の事後分布を求めてみましょう。イベント率の事前分布はbeta(1, 1);ですが、区間[0, 1]上の一様分布です。従って、事前には有効性に関して全く情報がない状態です。Stan, rstanの使い方に関しては、以前の投稿を参照してください。
ベイジアンアプローチによるリスク比の推定:Stan, rstanを用いて
#Bayesian estimation of risk ratio with event rates in intervention group and comparator group.
library(rstan)
# data 例:対照群 25/50、介入群 20/50、リスク比0.8
sampleSize <- 50
cevents <- 25
ievents <- 20
stan_code <- "
data {
int<lower=0> N; // 各群のサンプルサイズ(同じ)
int<lower=0> y_c; // 対照群イベント数
int<lower=0> y_i; // 介入群イベント数
}
parameters {
real<lower=0, upper=1> p_c; // 対照群イベント率
real<lower=0, upper=1> p_i; // 介入群イベント率
}
model {
// 非情報事前 Beta(1,1)
p_c ~ beta(1, 1);
p_i ~ beta(1, 1);
// 尤度
y_c ~ binomial(N, p_c);
y_i ~ binomial(N, p_i);
}
generated quantities {
real rr;
real log_rr;
rr = p_i / p_c;
log_rr = log(rr);
}
"
# コンパイル
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
bayes_rr_stan <- function(cevents, ievents, sampleSize,
iter = 50000, warmup = 25000, chains = 4) {
# Stan に渡すデータ
stan_data <- list(
N = sampleSize,
y_c = cevents,
y_i = ievents
)
# モデルをコンパイル
sm <- stan_model(model_code = stan_code)
# サンプリング
fit <- sampling(
sm,
data = stan_data,
iter = iter,
warmup = warmup,
chains = chains,
seed = 123
)
# 抽出
post <- rstan::extract(fit)
rr_samples <- post$rr
log_rr_samples <- post$log_rr
# 要約統計
rr_mean <- mean(rr_samples)
rr_median <- median(rr_samples)
ci_rr <- quantile(rr_samples, c(0.025, 0.975))
list(
fit = fit, # rstan オブジェクト(トレースプロット等に使える)
RR_mean = rr_mean,
RR_median = rr_median,
RR_CI95 = ci_rr,
RR_samples = rr_samples,
logRR_samples = log_rr_samples
)
}
# StanでMCMC実行
result <- bayes_rr_stan(cevents, ievents, sampleSize)
# 結果のコンソール出力
result$RR_mean
result$RR_median
result$RR_CI95
# 事後分布を可視化
#######Risk Ratio
hist(result$RR_samples, breaks = 50,
main = "Posterior of RR (Stan)",
xlab = "RR", col = "lightblue", border = "white")
dev.new()
hist(result$RR_samples, breaks = 50,
main = "Posterior of RR (Stan)",
xlab = "RR", col = "lightblue", border = "white",
freq = FALSE) # ★ 密度表示にするのが重要
# 密度曲線を追加
lines(density(result$RR_samples),
col = "red", lwd = 1)
text(1.5,1.5,paste("RR median =",round(result$RR_median,3)))
#######log Risk Ratio
dev.new()
hist(result$logRR_samples, breaks = 50,
main = "Posterior of RR (Stan)",
xlab = "RR", col = "lightblue", border = "white")
dev.new()
hist(result$logRR_samples, breaks = 50,
main = "Posterior of RR (Stan)",
xlab = "RR", col = "lightblue", border = "white",
freq = FALSE) # ★ 密度表示にするのが重要
# 密度曲線を追加
lines(density(result$logRR_samples),
col = "red", lwd = 1)
text(0.5,1.0,paste("log RR mean =",round(mean(result$logRR_samples),3)))
############################リスク比は以下の図の様になりました。iter = 50000, warmup = 25000, chains = 4なので、10万個の事後分布のサンプルです。リスク比の事後分布のサンプルの中央値0.8058、確信区間 0.5179~1.2334となりました。
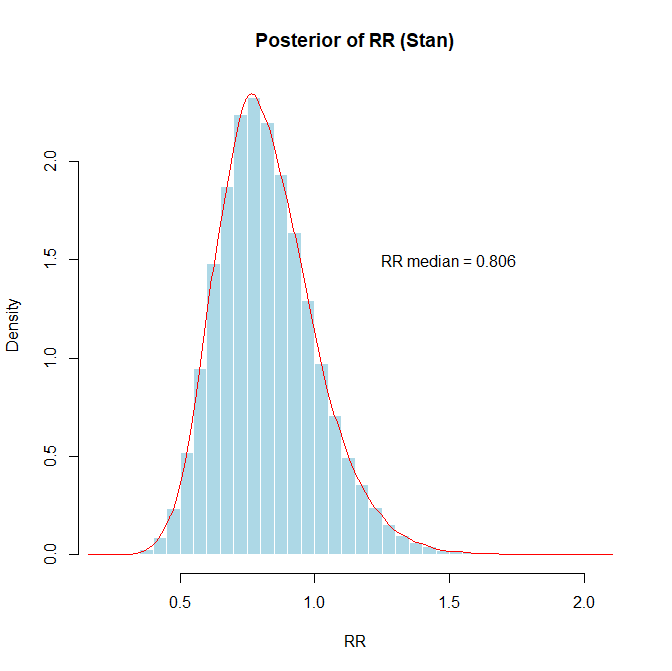
自然対数に変換すると、左右対称の分布となり正規分布に近似します。
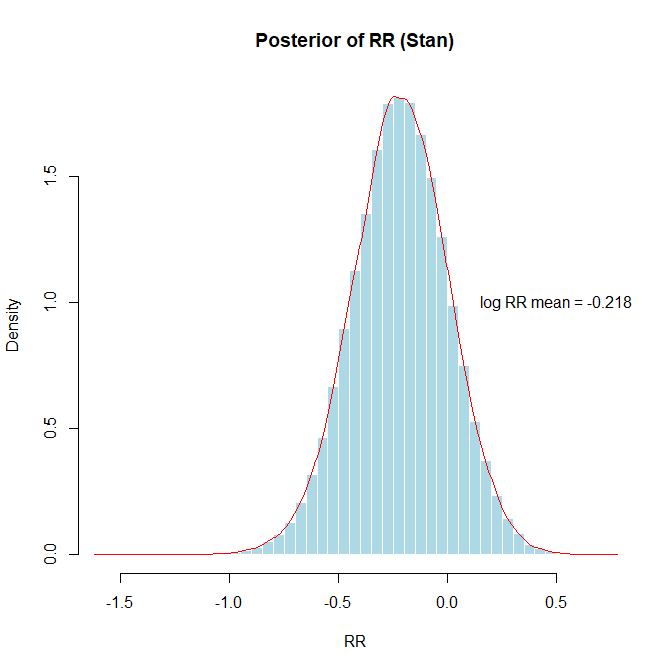
ベイジアンアプローチによるリスク比の分布でリスク比が1.0以上の確率は事後分布のサンプルから、mean(result$RR_samples >= 1.0)で求められます。0.15973でした。かなりの確率で介入群の方ででイベント数がより多くなることがあると考えられます。
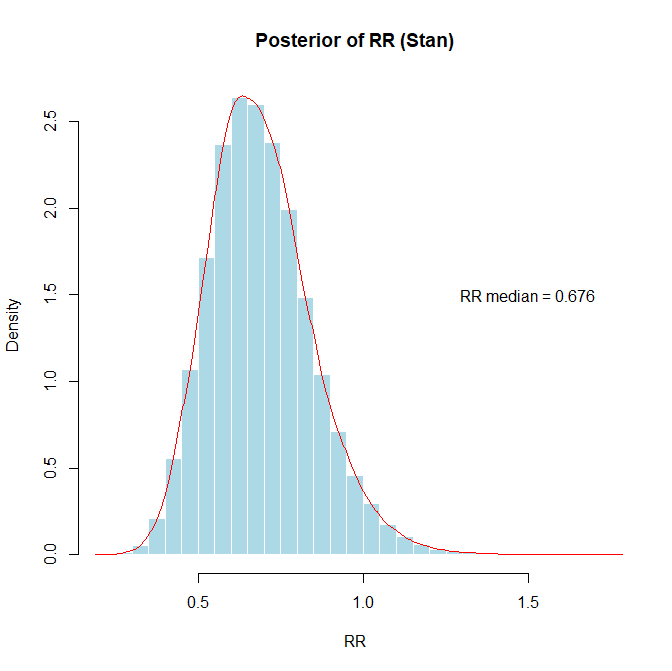
もし、対照群では50例中27例、介入群では50例中18例でイベントが起きたというデータを得たとします。その場合のリスク比の値は0.6899 (95%CI 0.4259~1.0334)でグラフで示すと以下の通りです。このCIはCredible Intervalです。mean(result$RR_samples <= 0.8)でリスク比が0.8以下の確率を求めると0.78でした。
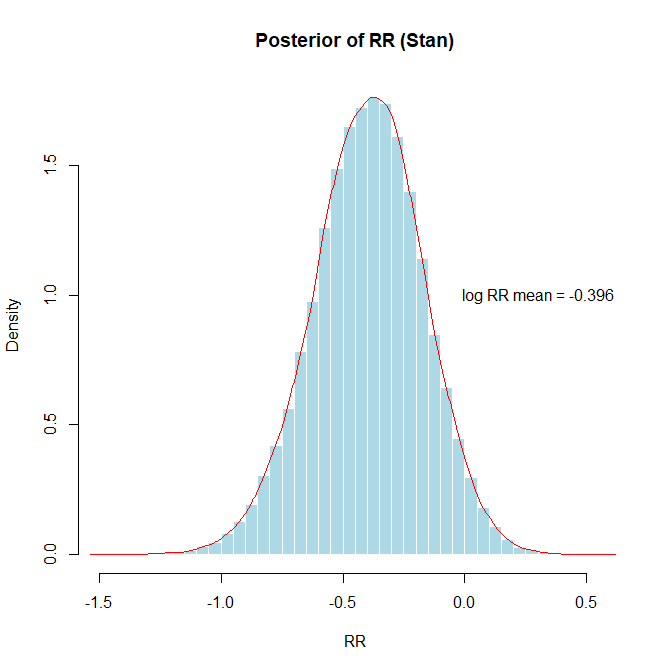
なお、自然対数に変換したグラフではlog RR mean = -0.396の描画の際text(0.3,1.0,paste(“log RR mean =”,round(mean(result$logRR_samples),3)))とx座標を少し左にずらしています。)
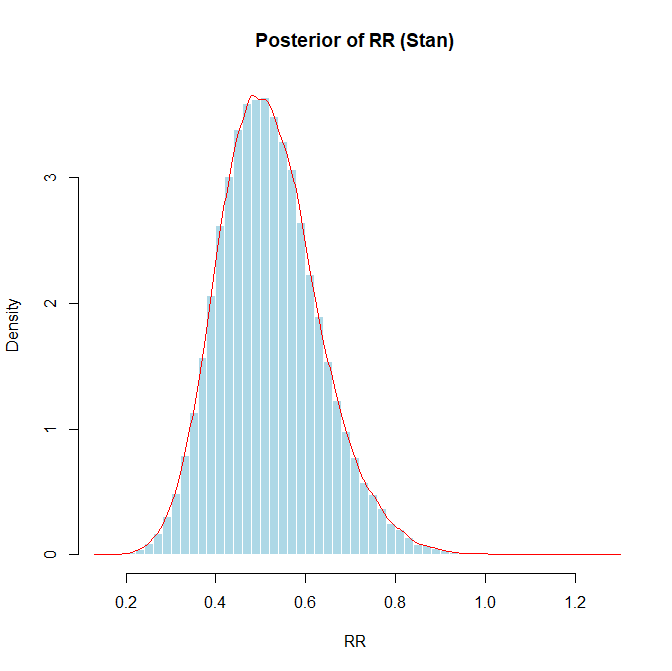
さらに、頻度論派アプローチで100個のリスク比をシミュレートした結果の内、95%信頼区間の範囲に真の値の0.8が含まれなかった例、対照群のイベント数34、介入群のイベント数17の場合のベイジアンアプローチでのリスク比を分析してみました。リスク比0.5192 (95%CI 0.3240~0.7603)となりました。リスク比が0.8以下の確率を求めると0.987でした。つまり、この95%確信区間には0.8の値は含まれないことが分かります。
メタアナリシスはほとんどの場合、頻度論派の手法が用いられていますが、統合値とその95%信頼区間の解釈で、ベイジアンアプローチの解釈の仕方をしないように注意する必要があります。
より分かりやすい解説をGamma.aiで作成してみました。こちらもご覧ください。
「頻度論派の信頼区間とベイズ統計の確信区間の違い」
以前作成したYouTubeの動画でも解説しています。
「信頼区間と確信区間の解釈:ベイジアンと頻度論派」

