このシリーズの1回目で絶対効果、Gail/NCIの方法、2回目では銀行口座の残高を”正味の益net benefit”に例えて、金額が効果の大きさ、為替レートがアウトカムの重要性に相当することを解説しました。この3回目では、架空の治療薬と4つのアウトカムから、正味の益を計算する方法を解説します。
最初にピクトグラム(図1)を見ながら考えてみましょう。
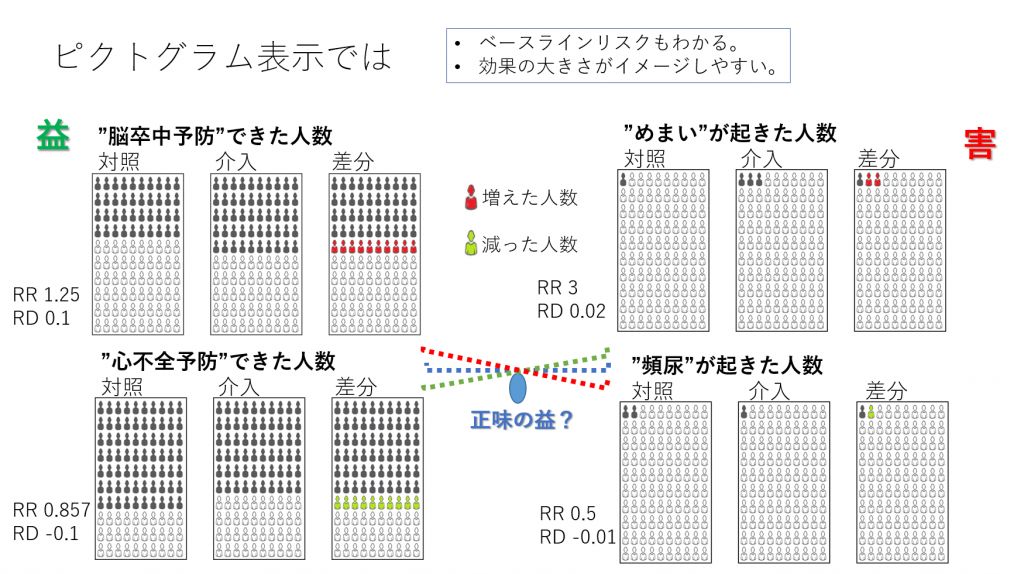
高血圧に対する薬物療法をモデルとして、2つの益のアウトカムと2つの害のアウトカムに対する2つの治療(介入と対照)の正味の益を分析してみます。介入と対照はいずれもアクティブな治療を想定しています。あくまで益と害の大きさとバランス=正味の益の分析を理解してもらうための単純化したモデルで、ベースラインリスクの高い集団が対象と考えてください。
益のアウトカムは脳卒中予防と心不全予防で、イベントとしては脳卒中発症と心不全の発症になります。10年間の累積発症率で介入と対照の正味の益の差を分析します。絶対リスクからそれぞれの治療の”絶対正味益”を計算してから、それらの差を求めることもできますが、今回はリスク差 Risk Difference(RD)を用いて、対照と介入の差を求めます。なお、いずれの方法でも得られる結果は同じになります。
これらイベントは時間経過の中で生起する事象なので、生存分析の対象になります。図1の左上の“脳卒中予防”できた人数のピクトグラムを見てください。このピクトグラムは発症予防できた人を黒塗りにしており、発症した人は白で表しています。したがって、対照では、10年間の累積発症率は白の人の割合で示され、0.6になります。指数関数モデルを用いた場合、10年間の累積発症率が0.6の場合、ハザード率Hazard rateは-ln(1-0.6)=0.916になります。すなわち、イベントフリーの割合の自然対数を求めて、-1を掛け算した値です。正負を逆にすることで、ハザード率の値が大きいほどより強いハザードにさらされていることになり、早くイベントが起きていきます。逆に、ハザード率が小さいほど弱いハザードにさらされていることになり、イベントはゆっくり起きていくことになります。ハザード率の大小関係とイベントの起きやすさが同じ方向になるので、わかりやすくなります。
さて、1年単位のハザード率は10乗したらイベントフリーの率である0.4になる値の自然対数です。10年単位のハザード率が0.9163なのでこれを10で割り算し、0.9163/10=0.09163が1年単位のハザード率になります。この値を正負を逆にして、Exponentialを計算するとexp(-0.09163)=0.9124が1年時の累積イベントフリーの率に相当します。0.9123を10乗すると0.4すなわち10年時のイベントフリーの率になります。0.9123を10乗する代わりに、1年単位のハザード率を10倍して正負を逆にしてExponentialを計算すると10年時のイベントフリーの率になります。累乗は対数変換すると足し算になるので、このようになります。
ここではt時点のイベント率pからハザード率hr=-ln(1-p)で計算されること、逆にハザード率からイベント率を求めるにはp=1-exp(-hr)で計算できることを覚えておきましょう。また、m時点のハザード率はhr*m/t、m時点のイベント率は1-exp(-hr*m/t)で計算できるということを頭の片隅に入れておきましょう。ハザード率はイベントフリーの割合の自然対数で-1を掛けた値です、と覚えるのもいいと思います。なお、ハザード比Hazard ratioはハザード率の比です。
さて、10年間で脳卒中を予防できた割合は対照で0.4、介入で0.5でした。100人あたりで考えると、対照では100人中40人で脳卒中を予防できたのが、介入では100人中50人で脳卒中を予防できたということになります。“脳卒中予防”というアウトカムでは、リスク差Risk Difference, RDは介入群の絶対リスクー対照群の絶対リスク=介入群のイベント率ー対照群のイベント率=0.5 – 0.4 = 0.1となり、リスク比Risk Ratio, RRは介入群の絶対リスク/対照群の絶対リスク=介入群のイベント率/対照群のイベント率=0.5/0.4 = 1.25となります。
“心不全予防”というアウトカムについては、10年間で心不全を予防できた割合は対照で0.7、介入で0.6でした。対照では100人中70人で心不全を予防できたのが、介入では100人中60人で心不全を予防できた。“心不全予防”というアウトカムでは、リスク差Risk Difference, RDは介入群の絶対リスクー対照群の絶対リスク=介入群のイベント率ー対照群のイベント率=0.6 – 0.7 = -0.1となり、リスク比Risk Ratio, RRは介入群の絶対リスク/対照群の絶対リスク=介入群のイベント率/対照群のイベント率=0.6/0.7 = 0.857となります。
ここで、アウトカムの内容について考えてみましょう。上記二つのアウトカムはいずれも有益事象です。つまり、それが起きることが望ましいアウトカムです。したがって、介入の方が望ましいと言える場合は、RDはプラスになります。この例では、脳卒中予防のアウトカムについては、介入側が望ましく、心不全予防というアウトカムについては、対照側が望ましいという結果になります。異なるアウトカムに対する効果にトレードオフTrade-offがあるということになります。介入側の治療を選択すべきか、対照側の治療を選択すべきか、RDの値だけで決めるのは難しいように思えます。
さらに、害のアウトカムも2つ考えなければなりません。害のアウトカムは“めまい”、“頻尿”で、いずれも有害な事象です。益のアウトカムと同様に、効果指標を計算してみましょう。“めまい”については対照群の絶対リスク0.01、介入群の絶対リスク0.03で、RD 0.02、RR 3となります。頻尿については、対照群の絶対リスク0.02、介入群の絶対リスク0.01で、RD -0.01、RR 0.5となります。
これら害のアウトカムでもトレードオフがあり、“めまい”では対照の方が望ましく、“頻尿”では介入の方が望ましいということになります。
それでは、4つのアウトカムに対する効果全体を考慮した上で、介入と対照のどちらを選択すべきでしょうか?脳卒中の方が重要だと思う人は介入側の治療、心不全の方が重要だと思う人は対照側の治療を選ぼうと思うかもしれません。そうです、ここでアウトカムの重要性によって望ましい選択肢が異なってくるらしいということは言えると思います。アウトカムの重要性をどのようにして決めるかは別として、アウトカムの重要性が臨床決断に影響するということは正しいであろうと言えそうです。そして、ピクトグラムを見せられても、介入と対照の治療の効果の差、ベースラインリスクを含む絶対リスクは直観的にとらえることができるが、意思決定はそれだけでは、難しということも言えそうです。
それでは、アウトカムの相対的重要性を設定し、図1の介入の効果の場合の正味の益を計算してみます。

この図2の例では、アウトカム1~4に対してリスク差RDとアウトカムの重要性を示しています。そして、RD×アウトカムの重要性を計算してから、それらの総和を計算し、アウトカムの重要性の合計で割り算しています。RDは介入群の絶対リスク-対照群の絶対リスクとして計算しています。
また、アウトカムが有益事象でRDがプラスで大きな値ほど望ましい場合は、正負は変えず、アウトカムが有害事象でRDがマイナスでより小さい値ほど望ましい場合は正負を逆にしてから総和を計算しています。マイナスでより小さな値とは、絶対値はより大きな値を意味します。例えば、アウトカム1の場合、“脳卒中予防”という有益な事象なので、RDがプラスで大きいほど望ましいと言えます。したがって、RD×アウトカムの重要性の値は正負を変えずそのまま総和を計算します。アウトカム2も同様です。アウトカム3は“めまい”という有害な事象なので、RDがマイナスでより小さい値ほど望ましいと言えます。したがって、RD×アウトカムの重要性の値は正負を変えて、総和を計算します。アウトカム4も有害な事象なので、3と同様に、正負を変えて総和を計算します。、
さらに、アウトカムの重要性は最も重要なアウトカムを100にし、最も重要でないアウトカムは0として、相対的に値を0~100の間に設定しています。アウトカムの重要性は個人の価値観によって決まるので、人によって結果が変わりえます。そして、上記の総和の計算の後、アウトカムの重要性の総和で割り算しています。これは、アウトカムの重要性の値を合計したら1になるように標準化と呼ばれる処理です。RDは1の値が最大で、‐1が最小になります。もし、すべてのアウトカムについてRDが1の場合は、その介入が最善となりますが、正味の益は1となります。このような処理を行うことにより、アウトカムの個数によらず、正味の益は0~1の範囲の値になります。
正味の益の計算式:K個のアウトカムの場合: *は掛け算を意味します。
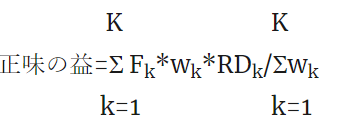
Fkはアウトカムの内容が有益事象の場合1、有害事象の場合-1とします。
この例では、対照に対して介入によって得られる正味の益は0.031となり、介入の方を選択すべきであるという結果になりました。なお、正味の益を100倍すると100人あたりで、正味の益を受ける人数になります。
さて、Gail/NCIの方法では、アウトカムの重要性を以下の様に3段階に設定しています。1列目の値をメインに用い、2~4列目の値は、感度分析に用います。
W1 Very important outcomes (life-threatening) 1 1 1 1
W2 Moderately important outcomes (severe) 0.5 1 1 0.5
W3 Not important outcomes (others) 0 1 0 0.25
次に、アウトカムの重要性をRDに掛け算する前に、標準化を行ってから計算してみます。結果は同じです。

アウトカムの重要性を標準化した場合でも、アウトカムが有益事象でRDがプラスで大きな値ほど望ましい場合は、正負は変えず、アウトカムが有害事象でRDがマイナスでより小さい値ほど望ましい場合は正負を逆にしてから総和を計算します。この点は先ほどの、標準化しないアウトカムの重要性で計算する場合と同じです。
正味の益の計算式:K個のアウトカムの場合。

Fkはアウトカムの内容が有益事象の場合1、有害事象の場合-1とします。
先ほどの計算と同じ結果が得られます。
この例では、正味の益はプラスで介入が望ましいことがわかりました。
難しそうに見えますが、リスク差(RD)はランダム化比較試験のシステマティックレビュー/メタアナリシスの結果から、アウトカムの重要性は個別に設定して、アウトカムごとにそれらの積(掛け算した値)を計算し、アウトカムが有害事象か有益事象かによって正負を設定して総和を求めるだけです。
次回は、より一般化したExcelの計算表を作成しようと思います。

