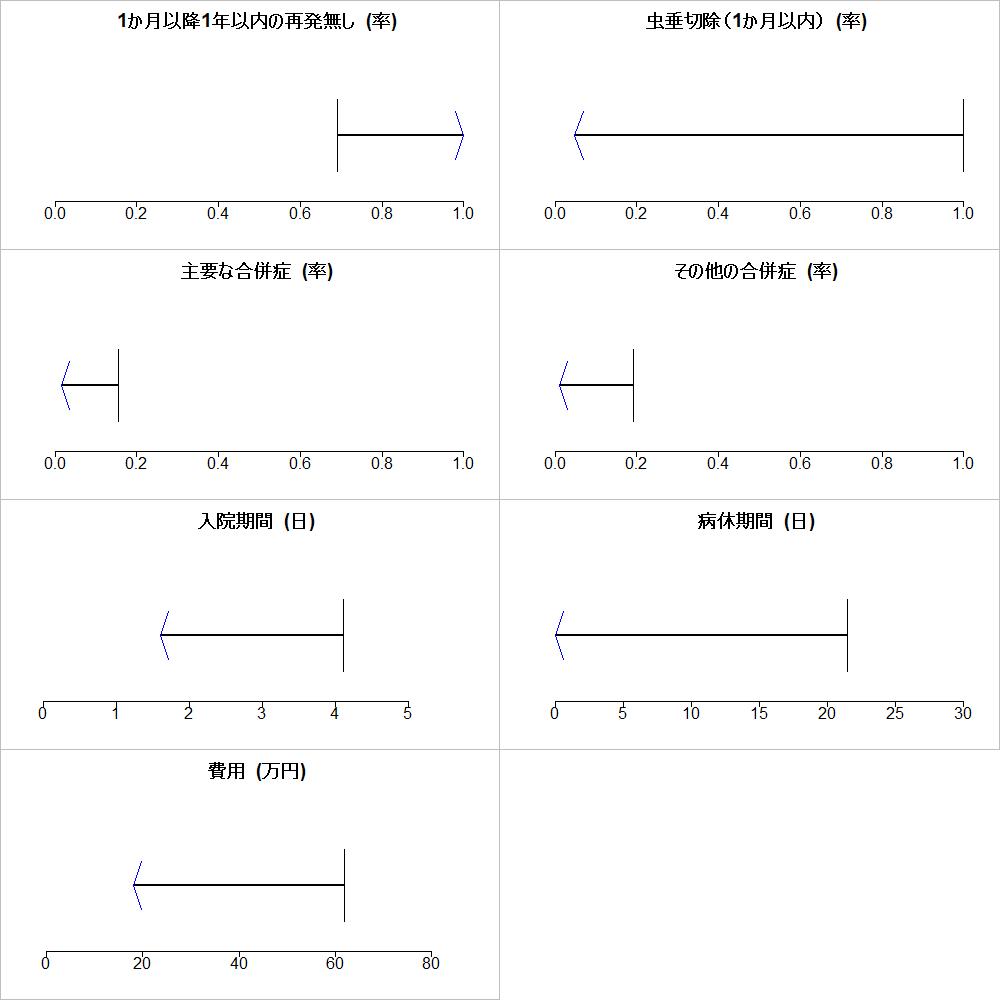
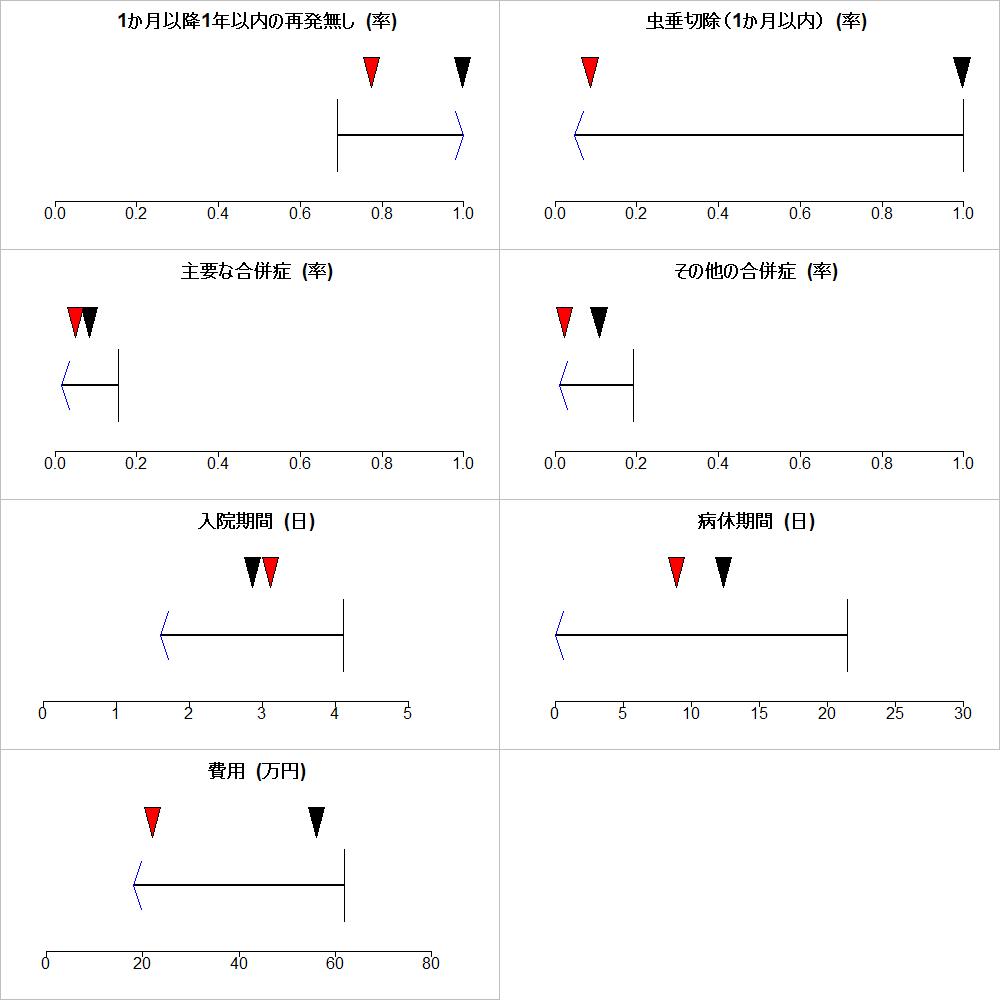
Keeney and RaiffaのMulti-Criteria Decision AnalysisあるいはMultiple Criteria Decision Analysis (いずれもMCDA)では評価項目Criteria=アウトカムOutcomeに対する介入の効果をパフォーマンスPerformance=効果推定値Effect estimateとして測定された値をそのまま用いるのではなく、スコア化Scoringして、共通の基準による大きさを表す値に変換する。変換のための関数を価値関数Value functionと呼ぶ。この方法では各アウトカムに対するさまざまな介入の効果の中で、最善のものと最悪のものを設定し、最善の場合はスコアが100、最悪の場合はスコアが0とし、実際の介入の効果はその間のいずれかに位置するようにして、スコア化する。値が大きい方がより良い場合と逆に値が小さい方がより良い場合があるが、いずれの場合にも対応できる。最善というのはありうる最も望ましい効果、最悪というのはありうる最も望ましくない効果と言い換えることもできる。
健康関連アウトカムだけでなく、費用も評価項目として扱うことができる。効果推定値は多くの場合システマティックレビュー/メタアナリシスの結果を用いる。また、個別患者の推定値を用いることもできる。
ただし、リスク比、リスク差などは対照群との相対的な比較に基づく指標であるが、MCDAでは各群のイベント率、平均値などが必要になる。一方で、3つ以上の介入を一度にに比較することが可能である。以下で効果推定値と述べているのはこれらイベント率、平均値であり、不確実性の指標としては標準誤差、標準偏差を用いる。
Bを最善Bestの効果を示す効果推定値、Wを最悪Worstの効果を示す効果推定値とし、Xをその介入の効果推定値とすると、スコアSは、S=(X – W)/(B – W) × 100で表される。XとSの間に直線関係がある場合は、この式で対処できる。直線関係以外の場合も、価値関数を作成すれば対応できる。従って、Keeney and Raiffaの方法では、それぞれのアウトカムに対する効果で最善のものは100、最悪のものは0になる。そのアウトカムに対するさまざまな介入の効果推定値の95%信頼限界のなかで、最小値と最大値をBまたはWとして用いることが可能である。また、理想の治療法を想定してBを想定することも行われている。比較する介入の中だけで、ローカルにB,Wを設定する場合と、すべての介入を考慮してグローバルにB,Wを設定する場合がある。スコアはそれぞれのアウトカムに対してありうる最善の効果と最悪の効果に対して、相対的な値として決められているため、アウトカムが異なっても、同じ効果の大きさを表していると言える。
スコア化に続いて、重みづけの値を決める。意思決定の際に、アウトカムそのものの重要性とそのアウトカムに対する介入の効果の大きさ=パフォーマンスPerformance=Effect estimateの両方を考慮すべきとされているが、重みづけの方法の多くは、たとえば、NCI/Gailの方法や、Analytic Hierarchical Process (AHP)の様に、アウトカムの重要性だけを評価している。それに対してKeeney and Raiffaの重みづけの方法はSwing weightingと呼ばれ、上記のB、Wの値の変動=スウィングを考慮した上で、アウトカムの重要性を考慮し、その両方で重みを決める。この重みは個人個人の異なる値に対応できるので、協働意思決定Shared decision makingにおいても用いることができる。
総スコアAggregate scoreは重みの値を標準化、すなわち各アウトカムに対する重みの値の合計値でそれぞれの重みの値を割り算した上で、各アウトカムに対するスコアに掛け算して合計することで求められる。これをそれぞれの介入に対して算出し、一番値の大きい介入が最も価値のある介入となる。介入間のスコアの差を求め、P値を算出することもできる。
なお、NCI/Gailの方法では、益のアウトカムに対してはプラス、害のアウトカムに対してはマイナスの値になる様に効果推定値を設定して、アウトカムの重要性を掛け算して合算するので、総計がプラスなら益>害、マイナスなら益<害と判定する。
Keeney and RaiffaのSwing weightingを用いたMCDAでは各効果推定値の不確実性、重みの不確実性に対応した確率的感度分析あるいは確率的シミュレーション分析も可能であり、さらに、異なるアウトカムに対する効果推定値の相関マトリックスと標準誤差あるいは標準偏差から分散共分散マトリックスを作成して、相関を取り込んだ解析も可能である。
このモデルは、重みづけ加算モデルであり、前提としては、1)それぞれのアウトカム(評価項目)の評価は他のアウトカムの評価つまりスコアと重みの値の影響を受けない、2)Vi > Vjの場合、介入iの方が介入jより望ましい、3)価値関数は間隔尺度(連続変数)である、4)スコア×重みの同じ値の変動は同じ価値の変動を表す、5)各アウトカムの重みは互いに影響しない、すなわち各アウトカムは独立している、6)各評価項目のスコアは互いに影響しない、各評価項目のスコアは相関していない、の条件が満たされる必要がある。
文献:
Keeney R, Raiffa H: Decisions with multiple objectives: Preferences and Value Tradeoffs. 1993, Cambridge University Press.
Marsh K, Goetghebeur M, Thokala P: Multi-criteria decision analysis to support healthcare decisions. Springer, 2017. (包括的な内容)
Thokala P, Devlin N, Marsh K, Baltussen R, Boysen M, Kalo Z, Longrenn T, Mussen F, Peacock S, Watkins J, Ijzerman M: Multiple Criteria Decision Analysis for Health Care Decision Making–An Introduction: Report 1 of the ISPOR MCDA Emerging Good Practices Task Force. Value Health 2016;19:1-13. PMID: 26797229 (この論文のAppendixにSwing-weightingの例が示されている)
Marsh K, IJzerman M, Thokala P, Baltussen R, Boysen M, Kaló Z, Lönngren T, Mussen F, Peacock S, Watkins J, Devlin N, ISPOR Task Force: Multiple Criteria Decision Analysis for Health Care Decision Making–Emerging Good Practices: Report 2 of the ISPOR MCDA Emerging Good Practices Task Force. Value Health 2016;19:125-37. PMID: 27021745
Wen S, Zhang L, Yang B: Two approaches to incorporate clinical data uncertainty into multiple criteria decision analysis for benefit-risk assessment of medicinal products. Value Health 2014;17:619-28. PMID: 25128056 (相関に対応。δ methodとMonte Carlo simulationによる方法を提示。価値関数がより単純化が可能の方法になっている。)
Broekhuizen H, Groothuis-Oudshoorn CG, van Til JA, Hummel JM, IJzerman MJ: A review and classification of approaches for dealing with uncertainty in multi-criteria decision analysis for healthcare decisions. Pharmacoeconomics 2015;33:445-55. PMID: 25630758 (ベータ分布を用いる)