Rはフリーの統計解析プラットフォームおよびプログラミング言語ですが、今は相当普及していて、アカデミアでも、使っている人が大勢いると思います。The Comprehensive R Archive NetworkではWindows版のみならずMac版、Linux版が提供されています。普段Windows10のノートPCを使うことが多いのですが、周りにはMacを使う人も多く、私自身も以前はMacを主に使っていました。今も時々iMacを使うことがあります。しばらくMacでRを使うことはなかったのですが、今日はMacでRの最新バージョンをインストールして、さらにXQuartzをインストールし、Bayesian推定に使われるJAGS (Just Another Gibbs Sampler)をインストールし、Rのパッケージであるrjagsとgemtcをインストールして、動かして見ました。
Network meta-analysisネットワークメタアナリシスにはすでに紹介したことのある、OpenBUGSが使われる事が多いのですが、ネットワークメタアナリシス用のRのパッケージであるgemtcとpcnetmetaはRからrjagsを介してJAGSを動かしてMarkov Chain Monte Carlo (MCMC) simulationを実行するようになっています。gemtcはコントラストベースcontrast-basedのネットワークメタアナリシス、pcnetmetaはアームベースarm-basedのネットワークメタアナリシスができるRのパッケージです。
rjagsとJAGSを使う事で、WindowsだけでなくMacでも同じようにデータ解析ができるというのが最大の利点だろうと思います。OpenBUGSはもともとWinBUGSと呼ばれていたもので、Windowsでしか動きませんが、JAGSは同じコードがMacでもWindowsでも動くので、Macの利用者のことを考えてこのような選択になったのだろうと思います。Windowsであれば、RからOpenBUGSを動かしてデータのやり取りをするにはBRugsというパッケージがあります。
Mac用のRはR-4.0.0.pkgでバージョンは4.0.0になっています(2020.5.22時点)。CRANのメインページから左サイドバーのMirrorsを開き、Japanのサイトのいずれかを選びます。Download R for (Mac) OS Xのページを開き、R-4.0.0.pkgをダウンドードして他のMac用ソフトと同じようにインストールします。続いて、同じページにあるXQuartzのリンクを開き、XQuartz-2.7.22.dmgをダウンロードしてインストールします。
JAGSは上記のリンクを開いて、Downloadsの項のfiles pageのリンクを開き、JAGSのリンクを開き、4.xを開き、MacOSを開いて、JAGS-4.4.0.dmgをダウンロードしてインストールします。JAGSはRとは独立したソフトウェアです。
これで後はRを起動して、Rのパッケージでであるrjagsとgemtcをインストールします。個別に、自分でRの”パッケージとデータ”メニュー から”パッケージインストーラ”を選んで、そこからインストールすることもできますし、以下のスクリプトをRのファイルメニューから新規文書で開かれるエディタに貼り付けて実行(command+return)することでもインストールする事ができます。その行にカーソルを置いてcommand+returnで実行されます。(Windowsだとctrl+rまたは実行ボタン)。packneed=c( )のパッケージ名を変更する事で他のパッケージのインストールにも使えます。
packneed=c(“gemtc”,”rjags”);current=installed.packages();addpack=setdiff(packneed,rownames(current));url=”https://cran.ism.ac.jp/”;if(length(addpack)>0){install.packages(addpack,repos=url)};if(length(addpack)==0){print(“Already installed.”)}
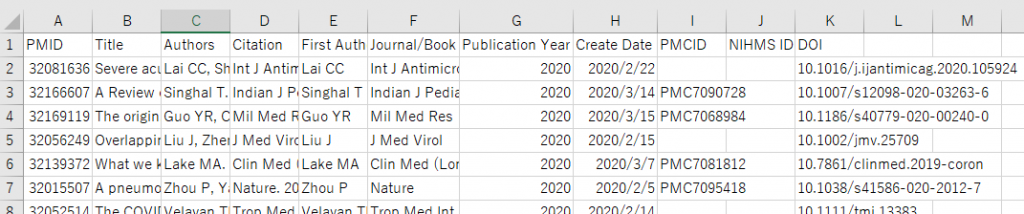
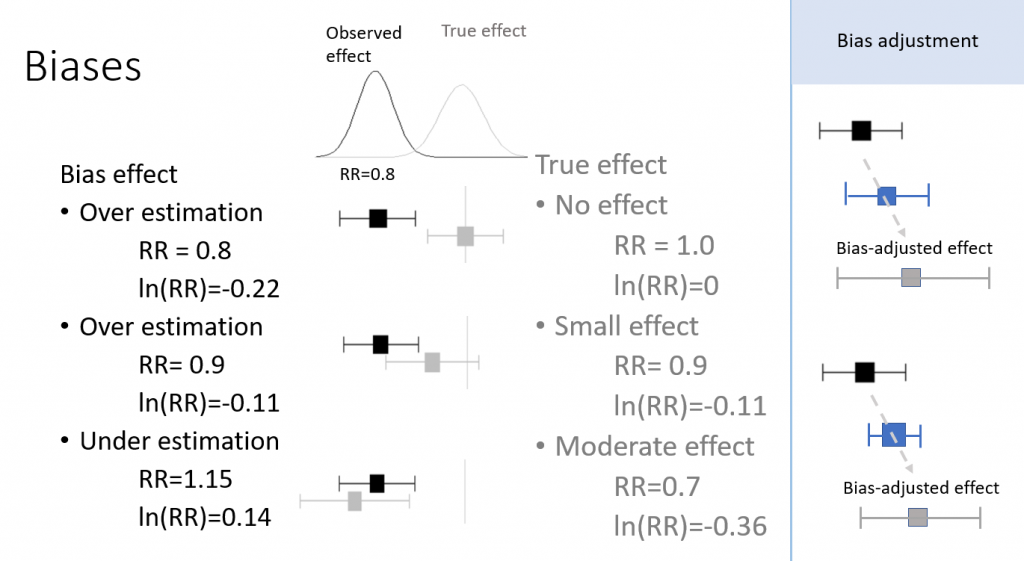
ここではuseRsで私が紹介しているgemtcを動かすスクリプトを実行した結果を示します。”#4. GeMTCを用いるベイジアンネットワークメタアナリシス”のScriptをクリックして出てくるバーのD:の右の四角をクリックするとクリップボードに内容がコピーされるので、Excelを開いて貼り付け、データを確認して下さい。サンプルデータの形式でデータを用意すれば、(上が二値変数、下が連続変数のデータサンプルです)。二値変数アウトカムでも連続変数アウトカムでもどちらも解析可能です。効果指標の値が小さいほうが望ましい場合は、上の#4-1のScript、値が大きい方が望ましい場合は、下の#4-2のScriptを使います。W:がWindows用、M:がMac用のスクリプトになっています。
この例は連続変数のアウトカムで、下のサンプルデータを用いています。Node-splittingモデルのプロットも出力するので、直接比較と間接比較の効果推定値のインコヒレンスincoherenceの評価がやりやすくなると思います。

自分でデータを用意するときは、Excelで同じ形式で用意し、データ範囲を選択し(この例ではセルA1からM11)、コピー操作をしてから、Rに戻り以下のいずれかのスクリプトを実行します(エディターのスクリプト上にカーソルを置いて、command+enterを押す)。上のスクリプトは値が小さい方が望ましい効果指標の場合、下のスクリプトは値が大きい方が望ましい効果指標の場合です。これらのスクリプトはuseRsでScriptをクリックして出てくるバーのM:の右の四角をクリックするとクリップボードにコピーされます。(Windowsの場合はW:の右の四角をクリックします)。
exdat=read.delim(pipe(“pbpaste”),sep=”\t”,header=TRUE);source(“http://zanet.biz/med/stat/ma/nma_gemtc_simpleL.R”)
exdat=read.delim(pipe(“pbpaste”),sep=”\t”,header=TRUE);source(“http://zanet.biz/med/stat/ma/nma_gemtc_simpleH.R”)
これらのスクリプトでは、私が利用しているウェブサーバーに置いてあるスクリプトのファイルをsource( )関数で読み込んで実行することでクリップボードにコピーされたデータに対して、データ処理、解析が行われるようになっています。スクリプトのファイルはhttpプロトコールでインターネットを介してダウンロードされ、そのままRで実行されます。Rは自分のPCに置かれているスクリプトファイルだけでなく、インターネットを介し別のサーバーに置かれているスクリプトを実行できる仕組みがあり、またデータもそのような仕組みで取り扱え、遠隔での共同作業がやりやすいようになっている点が素晴らしいと思います。
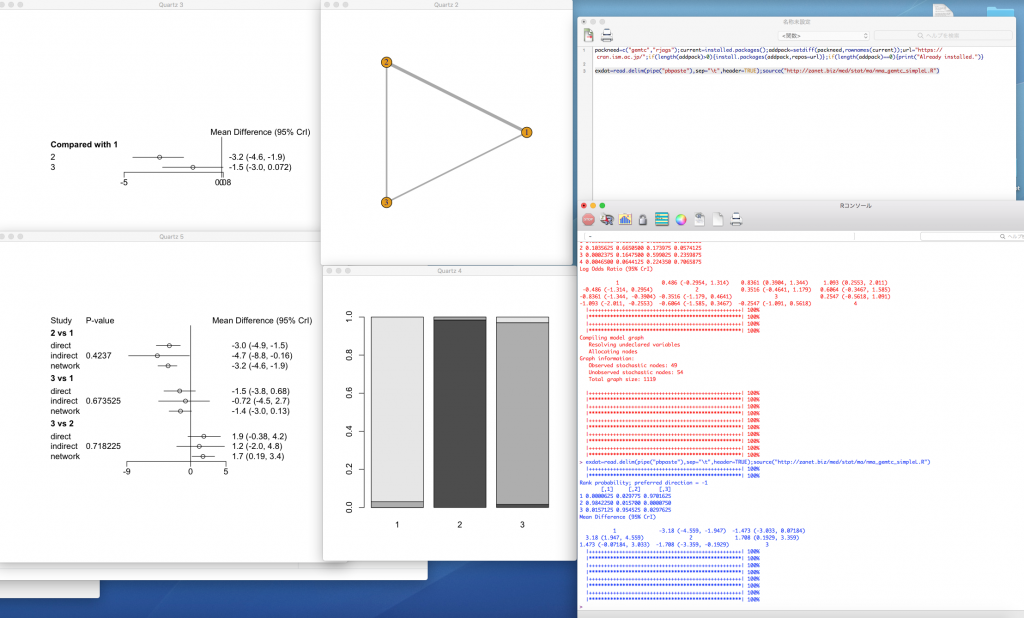
最後に、二値変数のアウトカムの場合のデータサンプルとそのネットワークグラフを示します。
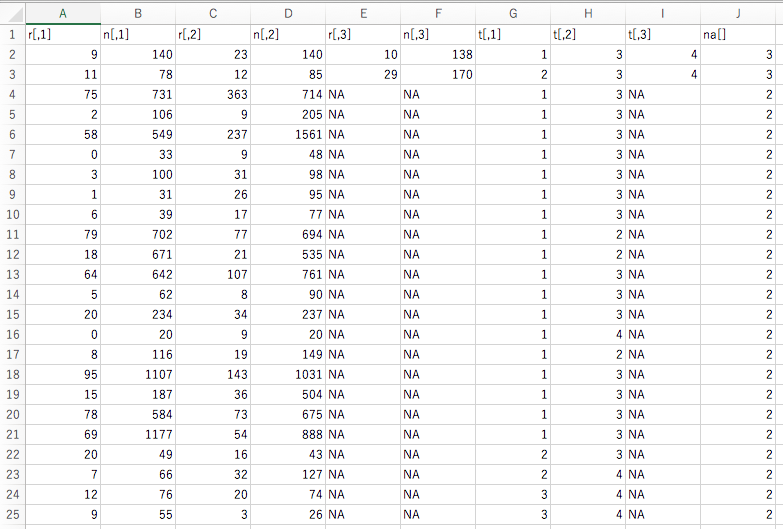
解析データは1行に一つの硏究のデータが含まれています。データの内t[,1], t[,2], t[,3]には治療番号のデータが入力されています。治療番号1が参照治療comparatorになります。必要に応じて、カラムや行を増やして使う事ができますna[]は治療アーム数です。
上の例では、2行目と3行目の研究は3アームで同時に3つの治療が比較されたランダム化比較試験です。それ以外の研究は2アームなのでt[,3]はNAになっています。行3,と行22の2つの研究は治療2と3を直接比較した研究です。治療2と3を治療1を介して間接比較できる研究は治療1と3を直接比較した行2, 4〜10, 13〜15, 18〜21の15研究と治療1と治療2を直接比較した行11,12,17の3研究があります。これら治療1と2の直接比較と治療2と3の直接比較から得られる効果推定値を差を求めることで、治療2と3の間接比較の効果推定値が得られることになります。そして、これら直接比較の効果推定値と間接比較の効果推定値の一致の程度を評価する事が必要になるので、ネットワークメタアナリシスに基づくエビデンスの確実性の評価は作業量が多くなり大変です。
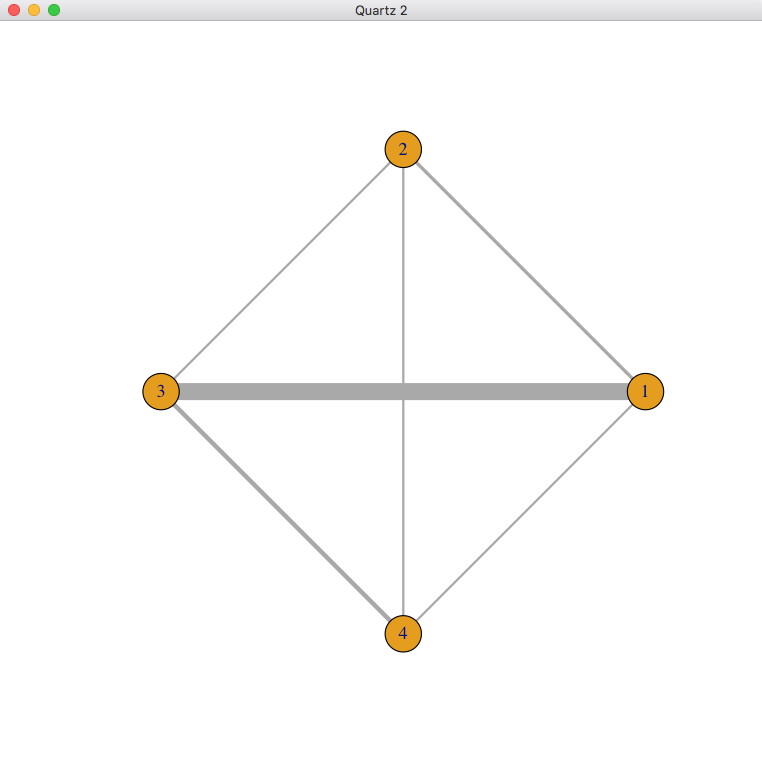
ネットワークグラフで閉じられたループがあると、直接比較の効果推定値だけでなく間接比較の効果推定値が得られる事がわかります。この例では、2と3を結ぶ線より、3と1を結ぶ線が太く、そこに多くの研究がある事が示されています。2と1を結ぶ線もあるので、2と3を比較する間接比較のデータが得られ、2と3を比較するネットワーク効果推定値には間接比較のデータがかなり影響するであろうと考えられます。実際、Node-splittingモデルのプロットを見ると、3 vs 2のnetwork estimateはindirectのestimateの影響で、オッズ比が0.93 (0.22-3.9)から1.4 (0.63-3.3)と大きな値になっています。
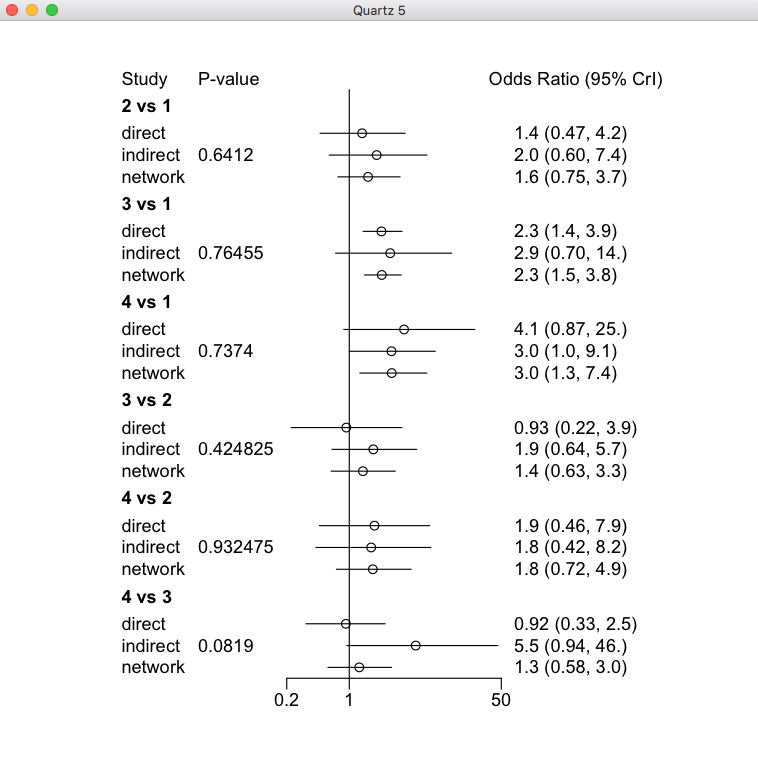
なお、この解析結果は#4-1のデータを#4-2のスクリプトで解析したものです。つまり、オッズ比の値が大きい方が望ましい結果です。Rankogramを見ると、治療4が最も治療効果が高い確率が最も高い事が言えます。しかし、上のNode-splittingモデルの4 vs 3の比較を見ると、間接比較の点推定値がかなり大きく、直接比較との間の検定ではP=0.0819ですが、バイアス、非直接性、非移行性intransitivityなどによって偏りが生じている可能性をチェックする必要があると言えます。

このようにネットワークメタアナリシスに基づくエビデンスの確実性の評価はかなりの作業量が必要となる事がわかります。ネットワークがもっと大きく、複雑になるとペア比較の数も多くなり、ネットワークの構造が複雑になり、間接比較と直接比較の効果推定値を比較する事も大変な作業になります。