Network Meta-analysisもだいぶ普及してきているけど、Arm-based modelというのが出てきて、今までの相対的効果指標を統合するという考え方がチャレンジを受けたような状態になっていると思う。
今までの主流はContrast-based modelですよね。
そうなんだ。しかも、ベースラインリスクについは、外部のデータを用いることが勧められていたりする。Dias SたちはそれをBaseline modelと呼んでいる*。
ランダム化比較試験の対照群のデータをそのまま使わない方がいいという考え方にも一理ある。ランダム化比較試験は対象者がセレクトされているから、Real worldでは違う絶対リスクである可能性は高いと考えられるから。しかも、個人個人はリスクが異なるから、リスク比のような相対的効果指標をメタアナリシスで統合して、それを適用して絶対効果を考えた方がいいという考えは理解できる。しかし、一方で絶対リスクをどのデータから求めるべきか?なかなか簡単にはいかない。
リスク比のような相対的効果指標の値はベースラインリスクが変わっても大きくは変動しないということが経験的データでも示されていて、メタアナリシスで統合されるそれぞれの研究のベースラインリスクが異なっていても相対的効果指標はほぼ同じになるはずだからそれを統合したほうがいいと思われて来た。
単純に論理的にのみ考えると、Arm-based modelは研究ごとのランダム割り付けを無視することになるという批判も正しいようにも思えるけど、実際にはそうでもないという反論もあって一概にはそうは言えないでしょう**。
まずはZhang J, et al: Network meta-analysis of randomized clinical trials: reporting the proper summaries. Clin Trials 2014;11:246-62. PMID: 24096635で出てくるArm-based modelのネットワークメタアナリシスのためのBUGSコードとデータ部分を示します。(こちらの論文もよく書かれています:Zhang J, et al: Bayesian hierarchical models for network meta-analysis incorporating nonignorable missingness. Stat Methods Med Res 2017;26:2227-2243. PMID: 26220535)
今日の目的はOpenBUGSを動かしてネットワークメタアナリシスを実行することなんだけど、このArm-based modelのネットワークメタアナリシスをやってみようと思う。OpenBUGSの使い方の第一歩は以前投稿しました。
(参考文献:
*Dias S, Ades AE, Welton NJ, Jansen JP and Sutton AJ: Network Meta-Analysis for Decision Making. 2018, John Wiley & Sons Ltd.
**Hong H, Chu H, Zhang J, Carlin BP: Rejoinder to the discussion of “a Bayesian missing data framework for generalized multiple outcome mixed treatment comparisons,” by S. Dias and A. E. Ades. Res Synth Methods 2016;7:29-33. PMID: 26461816)
model {
for(i in 1:tS) {
p[i]<-phi(mu[t[i]]+ vi[s[i], t[i]]) # model
r[i]~dbin(p[i], totaln[i]) # binomial likelihood
}
for(j in 1:sN){
vi[j, 1:tN]~dmnorm(mn[1:tN], T[1:tN,1:tN]) # multivariate normal distribution
}
invT[1:tN, 1:tN]<-inverse(T[,])
for (j in 1:tN){
mu[j]~dnorm(0, 0.001)
sigma[j]<-sqrt(invT[j, j])
probt[j]<-phi(mu[j]/sqrt(1+invT[j, j]))
#population-averaged treatment specific event rate
}
T[1:tN,1:tN]~dwish(R[1:tN, 1:tN], tN) # Wishart prior
for (k in 1:tN) {
rk[k]<- tN+1-rank(probt[],k) # ranking
best[k]<-equals(rk[k],1) # prob {treatment k is best}
}
for (j in 1:tN){ # calculation of RR, RD and OR
for (k in (j+1):tN){
RR[j, k] <- probt[k]/probt[j]
RD[j, k] <- probt[k]-probt[j]
OR[j, k] <- probt[k]/(1-probt[k])/probt[j]*(1-probt[j])
}
}
}
#DATA
list(tN=4,sN=24,tS=50,mn=c(0, 0, 0, 0),R=structure(.Data=c(1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1),.Dim=c(4,4)))
s[] t[] r[] totaln[]
1 1 9 140
1 3 23 140
1 4 10 138
2 2 11 78
2 3 12 85
2 4 29 170
3 1 75 731
3 3 363 714
4 1 2 106
4 3 9 205
5 1 58 549
5 3 237 1561
6 1 0 33
6 3 9 48
7 1 3 100
7 3 31 98
8 1 1 31
8 3 26 95
9 1 6 39
9 3 17 77
10 1 79 702
10 2 77 694
11 1 18 671
11 2 21 535
12 1 64 642
12 3 107 761
13 1 5 62
13 3 8 90
14 1 20 234
14 3 34 237
15 1 0 20
15 4 9 20
16 1 8 116
16 2 19 146
17 1 95 1107
17 3 134 1031
18 1 15 187
18 3 35 504
19 1 78 584
19 3 73 675
20 1 69 1177
20 3 54 888
21 2 20 49
21 3 16 43
22 2 7 66
22 4 32 127
23 3 12 76
23 4 20 74
24 3 9 55
24 4 3 26
END
上のブロックをすべて選択して、コピーして、OpenBUGSを立ち上げて、FileメニューからNewを選んで、エディター画面に貼り付けました。
そうそう。そしたら、下の図のように、ModelメニューからSpecification…を選んで、Specification Toolを表示させ、コードのmodelの文字列を選択して反転した状態で、Specification Toolのcheck modelボタンをクリックします。
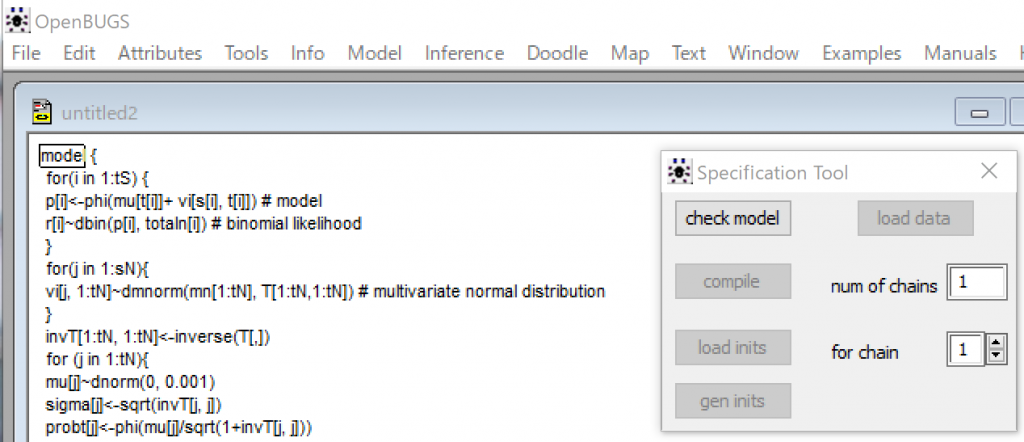
ボトムバーにmodel is syntactically correctと表示されました。確か次のステップはデータの読み込み、load dataでしたよね。
そうそう。#DATAのlistの文字列を選択して反転させて、Specification Toolのload dataボタンをクリックしましょう。
listをダブルクリックしたら、Specification Toolのload dataボタンがアクティブになりました。クリックしました。あっ、ボトムバーにdata loadedと表示されました。
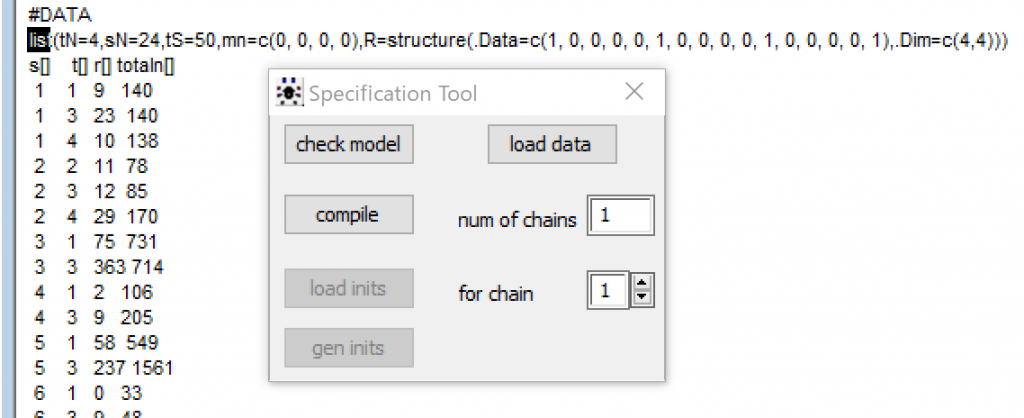
それでは次に解析対象のデータを読み込ませます。このデータはRのパッケージであるpcnetmetaやいろんなパッケージに付属している禁煙治療のランダム化比較のデータです。
研究数は24件、治療の数は4種類(1) no contact (NC); 2) self-help (SH); 3) individual counselling (IC); 4) group counselling (GC)で、治療アームの数は50です。一行がひとつの治療アームです。コードの#DATA中のtNが治療の数、sNが研究数、tSが比較ペアの数、に対する変数名になってます。治療の種類は次のデータ部分のt[]という変数に1~4の整数で指定されています。研究番号は同じくs[]という変数で表してます。
このデータソースはHasselblad V (1998) “Meta-analysis of multitreatment studies.” Med Decis Making 18(1), 37–43. だそうです。
なるほど。残りのデータは表形式みたいですね。確か、Excelで用意して、コピーして、OpenBUGSのEditメニューからPaste Special…でPlain Textで貼り付けるんでしたね。
その通り。で、s[]から一番下のENDの最後まで選択して、反転させ、Specification Toolのload dataボタンをクリックしてください。
やりました。ボトムバーにdata loadedと表示されたので、Specification Toolのcompileボタンをクリックします。
ボトムバーにmodel compiledと出ました。
load initsとgen initsボタンがアクティブになりましたね。
今回は、初期値の設定のためのデータを特に用意していません。事前分布の値priorをサンプリングする場合、幅広い分布の場合、初期値を設定しないと、非常にはじっこの方の値が得られた場合、Markov Chain Monte Carlo (MCMC)によるGibbsサンプリングがうまく動かなくなることがあるので、そのような場合は、初期値の設定用のデータを用意した方がいいです。書き方は、#DATAのlist()と同じような書き方です。
今回は、T[1:tN,1:tN]~dwish(R[1:tN, 1:tN], tN) # Wishart priorのコードの部分で、マトリックスデータRからWishart分布のランダムサンプリングを行って、マトリックスTに格納する操作をしているので、いずれにせよgen initsの実行が必要になります。load initsなしで、gen initsを実行すると、すべてのランダムサンプリングが実行され、それらの値からMCMCが開始されることになります。
gen initsボタンをクリックしたら、ボトムバーにinitial values generated. model initializedと出ました。
次は、ModelメニューからUpdate…を選んで、Update Toolでupdatesの回数を設定するんでしたね。10000回に設定してみました。それで、updateボタンをクリックしてバーンインを実行します。

あっという間にバーンインが終了しました。
次は、サンプリングした値を記録する変数nodeを設定するんでしたね。InferenceメニューからSamples…を選んで、Sample Monitor Toolを表示して、nodeの右のフィールドに、probtと入力して、setボタンをクリックします。続けて、RR、RD、OR、rk、bestと入力して順次setボタンをクリックしました。全部で6個の変数です。
probtは各治療群の絶対リスクAbsolute risk、RRは各治療ペアでのリスク比、RDは同じくリスク差、ORはオッズ比、rkは各介入が1、2位…の確率、bestは各介入が最善である確率ですね。
その通り。それでは、サンプリングの個数を50000に設定して、つまり、Update Toolのupdatesを50000に変えて、updateボタンをクリックしましょう。
今度は30秒くらいかかりました。結果を見るには、Sample Monitor Toolでnodeのフィールドに*を入力してstatsボタンをクリックするんでしたね。これで、記録された全部の変数nodeの平均値、中央値、95%確信区間などの値が表示されるはずですよね。
出ました。
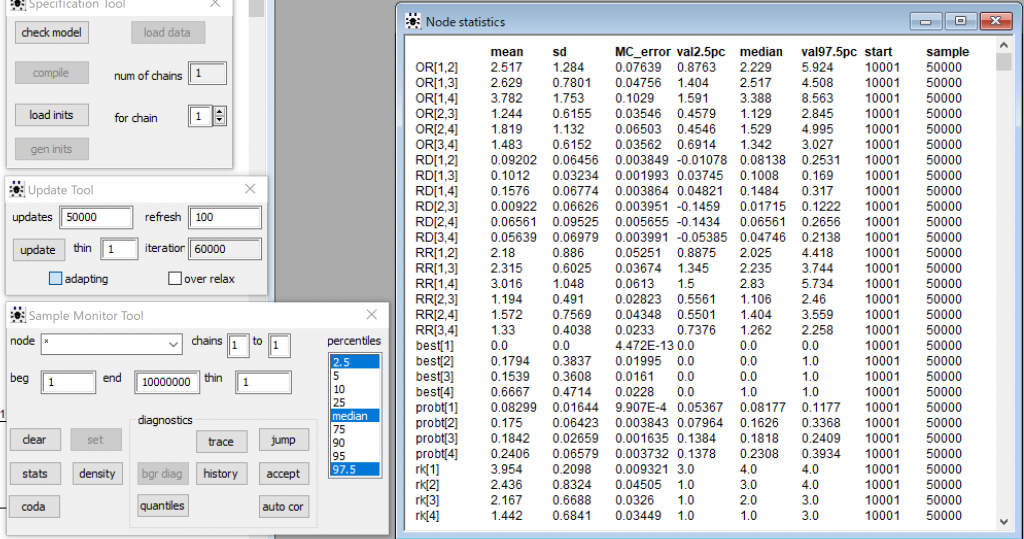
この結果で、Arm-based modelの特徴として、各治療群の絶対リスクAbsolute riskが得られるということがあげられます。このデータでは、probtの値が大きい方がよい結果です。つまり禁煙成功率が高いということです。
治療4が一番成績がいいことが分かりますね。これはGroup counsellingが禁煙効果が最も高いということですね。best[4]の平均値が0.6667なので、治療4が最善である確率がおよそ0.67であることが分かります。
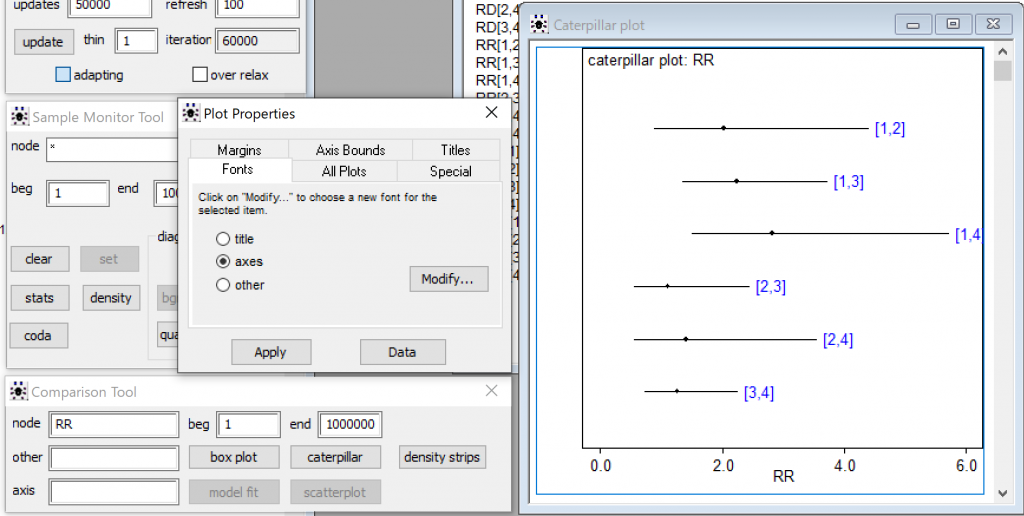
なるほど、RR, OR, RDについてはすべてのペア比較の値が出てますね。
InferenceメニューからComparison Tool…を選んで、Comparison Toolを表示して、nodeにRRと入力して、caterpillarプロットを表示してみました。プロットを右クリックして、Propertiesからフォントを変えたりしてみました。
probtとRRのdensity(確率密度分布)も表示してみました。

リスク比はそのままだと、正規分布ではないですね。対数変換すると左右対称の分布になるはずです。
さて、今回はArm-based modelを用いたNetwork Meta-analysisをOpenBUGSで行いました。同じ解析をRのパッケージであるpcnetmetaを使って実行することができます。同じ結果が得られるはずです。nma.ab.bin()という関数を使うんだけれど、model=”het_cor”にした場合、今回のモデルと同じになります。pcnetmetaでは、下のような、Network Graphも作成できます。
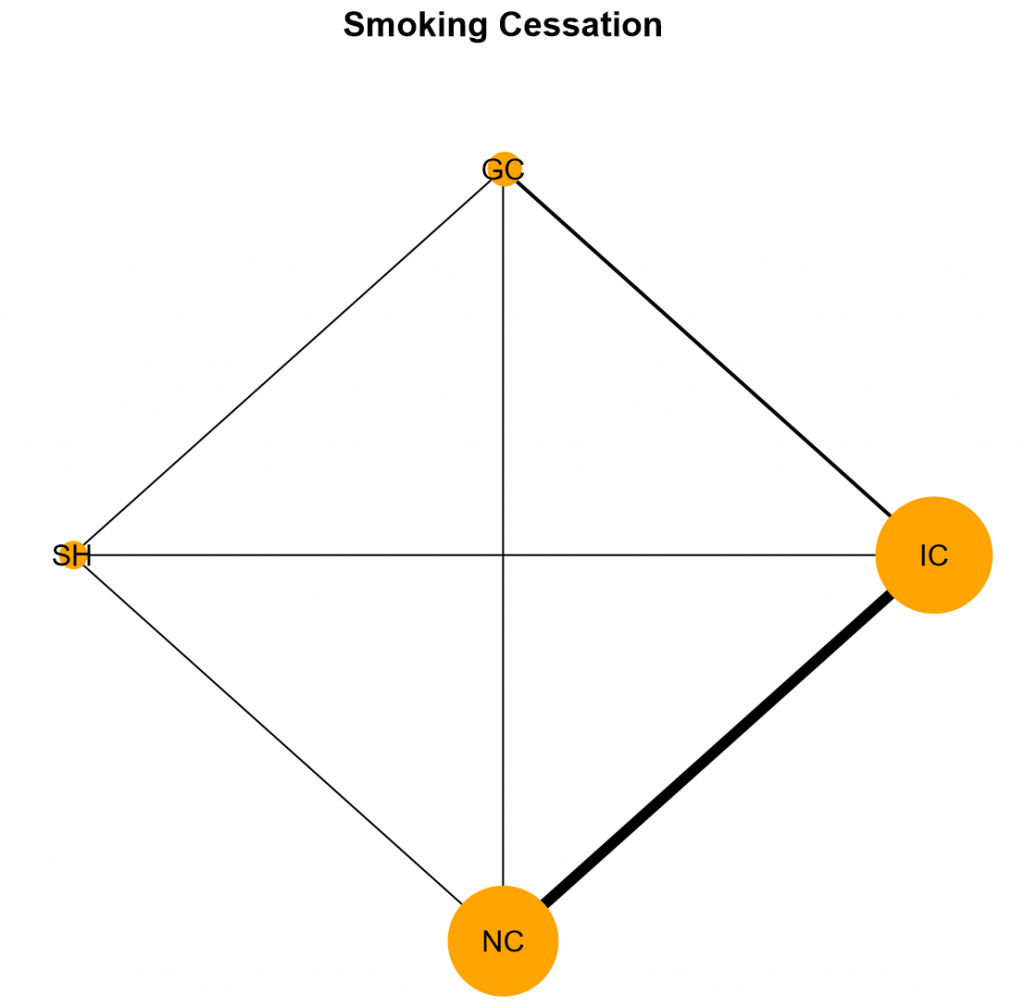
pcnetmetaだけでなく、RのパッケージのプログラムやデータファイルはGitHubで見られるんですね。これってすごいですね。
今回は、OpenBUGSの動かし方についての説明だけで、Network Meta-analysisの統計学的モデルの説明はしなかったけれど、本当はそっちが重要ですね。Arm-based modelは今までの、通常のペア比較だけのメタアナリシスに対しても適用できて、しかも単一群のつまりSingle-armのコホート研究や疾患レジストリーのデータなども活用できる可能性がある。Zhang J, et al: Bayesian hierarchical methods for meta-analysis combining randomized-controlled and single-arm studies. Stat Methods Med Res 2019;28:1293-1310. PMID: 29433407の論文でわかるよ。それと、間接比較の際に、欠損値の補完という考えを適用するというHong Pらの方法も画期的ですね。Hong H, et al: A Bayesian missing data framework for generalized multiple outcome mixed treatment comparisons. Res Synth Methods 2016;7:6-22. PMID: 26536149
これはすごい進歩ですね。本当に。まだまだ議論が続きそうな気配ですね。問題は、直接比較と間接比較のインコヒレンスだけではないですね。
最後にArm-based modelとContrast-based modelを式で表したものを見せるね。



