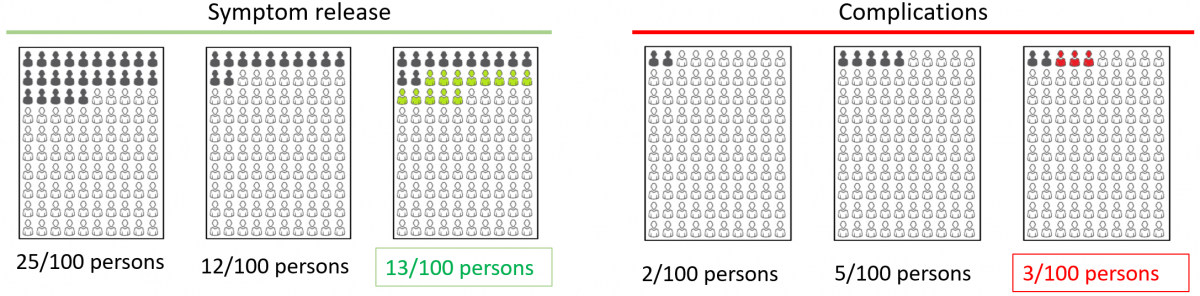
Linear combination of n variables with normal distributions with weights. 重みを係数coefficientsと言い換えてもいいです。
すぐにはピンとこないかもしれませんが、例えば、日本人の夫婦の身長の合計、つまり二人の身長の合計の平均値と分布を知りたいとします。それぞれ夫と妻の身長の分布が正規分布に従っているとします。日本人の夫の身長の平均値と分散、分散は標準偏差の二乗です(個々の値と平均値の差の二乗値の平均値が[標本]分散です)、が分かっていて、妻の身長の平均値と分散が分かっているとします。夫と妻のペアはランダムな組み合わせだとすると、(実際には背の高い妻は背の高い夫がいるというようなある程度の相関があるかもしれませんが、まずは妻と夫の身長の間にはそのような相関が無い、つまり共分散が0と仮定しておきます)、夫の身長と妻の身長の合計値の分布はどうなるでしょうか?平均値はそれぞれの平均値の和になり、分散はそれぞれの分散の和になります。
日本人の妻の集団からランダムに一人抜き出し、日本人の夫の集団からランダムに一人抜き出し、かれらの身長を測って、合計するということを繰り返した場合、その合計値の分布はどうなるかという風に考えてみて下さい。
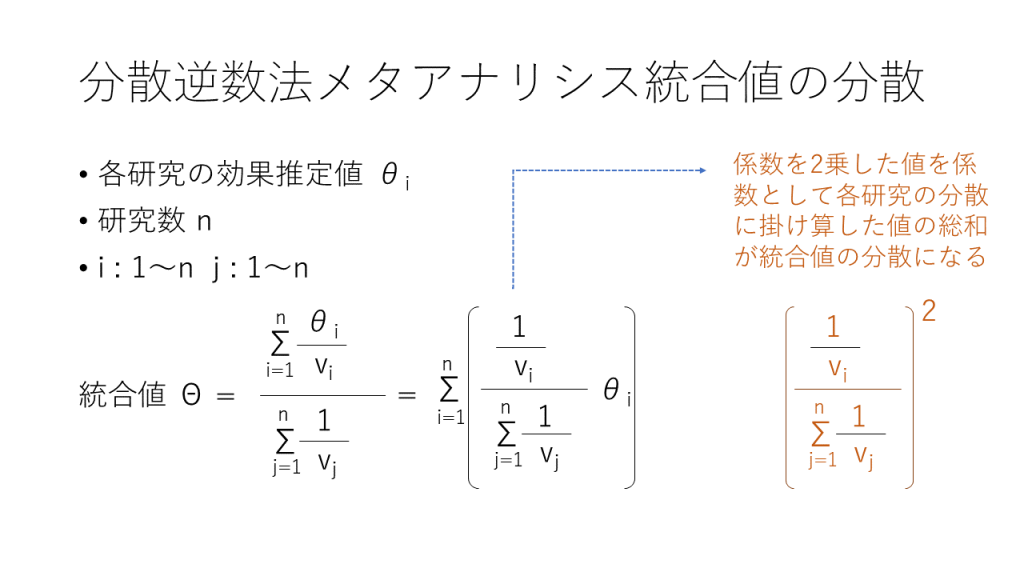
このような計算がどいう時に使われているかというと、突然話が飛びますが、例えば分散逆数法Inverse-variance methodによるメタアナリシスの際に統合値の分散を求める際に使われています。計算法を図1に示します。今度は、妻と夫の身長という二つの変数ではなく、研究の数分の変数を扱います。

一つの研究の効果推定値(リスク比、オッズ比、ハザード比の自然対数、連続変数であれば平均値)に対して、その分散の値の逆数を重みとして掛け算して、その総和を重みの総和で割り算すると統合値が得られます。
その統合値の分散を計算するにはどうするか?分散の逆数の総和の逆数をΣの内側に移動させることができるので、各研究の効果推定値に掛け算される値は、その総和で各研究の重みの値、つまり、各研究の効果推定値の分散の逆数を割り算した値になります。これが、係数として各研究の効果推定値に掛け算されているとみなせます。そして、統合値の値の分散はこの係数の二乗値を各研究の効果推定値の分散に掛け算した値の総和になります。
ただし、各研究の効果推定値は独立していて、相関が無いことが前提です。また、それぞれの効果推定値は正規分布に従うことが前提です。つまり、リスク比、オッズ比、ハザード比の自然対数、連続変数であればその値が、正規分布に従うことを前提としています。
さて、正規分布に従う複数の変数に重みの値を掛け算した値の総和の分散のより一般化した計算法を図2に示します。

各変数のペアで相関がない場合で、この図で示すCov、つまり、共分散の値が0の場合が、上で述べた計算です。図2の2つ目と3つ目の式でCov(Xi,Xj)=0となるので、各研究の効果推定値に係数の二乗を掛け算した値の総和が統合値の分散になります。また、係数aiが1で共分散が0の場合は、それぞれの変数の分散を合計すればXiの合計の分散になります。最初に述べた、妻と夫の身長の和の分布の分散の計算の場合はこれに相当します。
メタアナリシスの分散逆数法の統合値の分散は各研究の分散の逆数の総和の逆数になりますが、実は、ここで二つの図で示した計算式から証明することができます。図3、図4にそれを示します。

また、これらの計算には、分散共分散行列を計算に用いることもでき、変数間に相関がある場合にも対応できます。その際には、行列計算の知識が必要になります。
今回解説した、係数を掛け算した正規分布に従う変数の平均値の分散の計算は価値観で重みづけした効果推定値の総和、すなわち正味の益(net benefit, benefit-harm balance)の分散の計算でも、バイアス効果で調整した統合値の分散の計算でも用いられます。
一般化した言い方をすると、”正規分布に従う複数の変数に重みの値を掛け算した値の総和の分散”ということになります。重みづけ平均値とあわせて理解しておく必要があると思います。
そして得られた分散の値の平方根に1.96を掛け算してブラスマイナスすると95%信頼区間が得られます。さらに、例えば正味の益が0以上の確率やある閾値以上の確率を計算することもできます。