ベースラインリスクがどれくらい高かったら治療を開始すべきか?についてDjulbegovic Bらのアプローチを前投稿で紹介しました。彼らの方法では、疾患確率を1.0に設定して、ベースラインリスクの値を変動させた場合に、益が害を上回るベースラインリスクの値を算出します。
別の観点から見ると、疾患確率とベースラインリスクのふたつの変数によって益と害の大きさが決まり、益の大きさが害を上回る疾患確率の値と、ベースラインリスクの値が治療閾値になるということになります。Djulbegovic Bらの論文の例に対して、疾患確率とベースラインリスクの両者を含む決定木Decision treeを作成してみました(図1)。
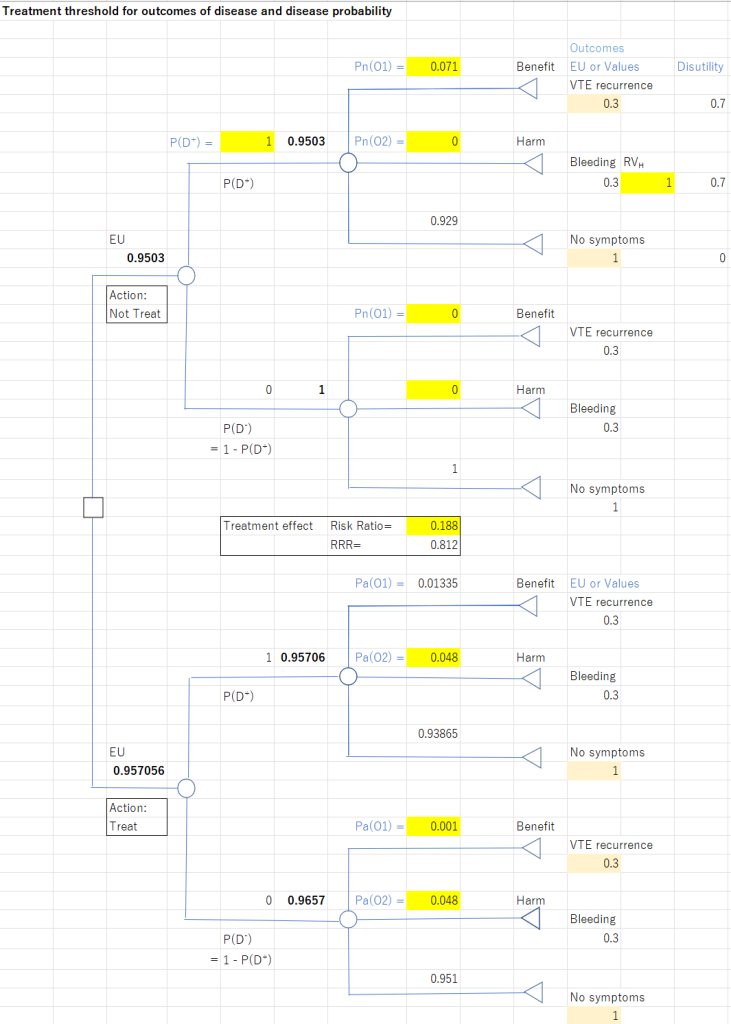
この決定木は治療を選択した後、P(D+)の確率で疾患が起き、その後VTE再発、出血、無症状の枝に分かれ、それぞれが図中に示す確率で起きることをモデル化しています。こうすることで、疾患確率=P(D+)とベースラインリスク=VTE再発確率Pn(O1)の二つの変数を変動させた場合の効用値を治療しない場合と治療する場合で比較することができるようになります。
この決定木に基づいて、治療閾値を計算する方法を図2に示します。VTE再発が治療によりリスク比(RR)0.188で抑制され、一方で出血の副作用が治療により4.8%起きます。期待効用は何も起きない場合を1.0とし、VTE再発は0.3、出血は0.3とし、これら二つのアウトカムの重要性(Values)は1:1、すなわちRVHを1に設定してあります。
図中の疾患確率に基づく治療閾値はベースラインの値を固定して、疾患確率を変動させることで、また、アウトカムの発生確率に基づく治療閾値は疾患確率を1に固定して、ベースラインリスクを変動させることで、計算しています。
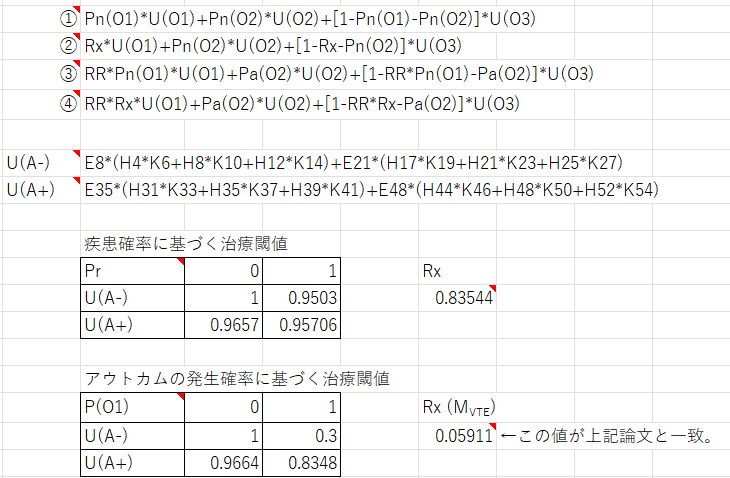
図2の右下にアウトカムの発生確率に基づく、すなわち、ベースラインリスクがいくつになれば益が害を上回るかを示していますが、0.05911と前回と同じ値が得られています。
通常の決定木Decision treeのモデルは今回示したものだと思いますし、このモデルの方が理解が容易だと思います。
Excelのシートのサイズが大きく、式も多いので、詳細はこちらからファイルをダウンロードして見てください。Download
文献:
Djulbegovic B, Hozo I, Mayrhofer T, van den Ende J, Guyatt G: The threshold model revisited. J Eval Clin Pract 2019;25:186-195. doi: 10.1111/jep.13091 PMID: 30575227

