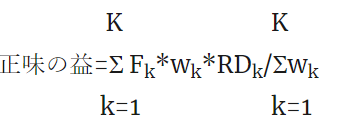治療閾値について理解するためには、期待効用、疾患確率についての知識が必要になります。
疾患確率は、その人が想定する疾患に罹患している確率です。ここではP(D+)で表しています。確率ですから、0~1の値を取ります。100人の人がいて、その内の50人がある疾患に罹患しているとします。その100人の中から、1人が特別な理由なく、やってきました。その人がその疾患に罹患している可能性はどれくらいでしょうか?それを疾患確率と言います。この場合は、0.5です。
Utilityユティリティ(効用)をNeumann PJらは次のように定義しています。“A utility is a measure of preference. In this context a utility is the measure of the preference or value that an individual or society places upon a particular health state. ” (Neumann PJ 2017) つまり、“特定の健康状態に個人または社会が置く好みまたは価値を測定した値”を効用と呼びます。値については、効用値という用語が用いられる場合もあります。また、個人の考える効用値は個人個人で異なり、個人の考える効用値と社会を代表する効用値は異なる場合もあります。なお、経済学では商品、サービスに対する好み(選好)を効用と言っています。
Expected Utility 期待効用と言う場合は、その健康状態が実現する前の時点で述べる場合の表現です。

図1では、Uが期待効用を表しており、カッコ内にその条件を疾患の有無をD、治療またはアクションをAで表しています。例えば、U(D+A–)は疾患Dがあり検査も治療も受けない場合の期待効用を表しています。
期待効用の大きさは0~1の値で表され、0は死亡、1は疾患が無く、検査も治療も受けない状態に対応します。したがって、U(D–A–)=1となります。
期待効用はある健康状態についてどれくらい価値があると思うかを0~1の数値で表したものということもできます。それぞれの価値観に基づく価値の大きさと言えます。
図1は、治療をしない場合の期待効用U(A–)と疾患確率P(D+)の関係を決定木を用いて解析するためにExcelを用いて作成したものです。治療をしない場合の期待効用U(A–)は枝の終末の期待効用の値にその枝の起きる確率を掛け算して総和を求めることで計算されます。下の方の式で示すように、U(D–A–)とU(D+A–)を設定すると、その差の負の値を係数とし、U(D–A–)を切片とする疾患確率P(D+)の一次関数linear functionで、U(A–)が計算されることが分かります。
疾患確率と期待効用は直線関係にあるということが分かります。
係数が負の値であるということは、疾患確率が高まるほど、期待効用が低下することを示しています。例えば、その疾患に罹患している人が100人いて、治療をしないで放置した場合、100人全員に疾患による望ましくないアウトカムが起き、U(D+A–)で表される期待効用は1よりは小さな値になります。これは疾患確率P(D+)が1の場合に相当します。もし、その疾患に罹患していない人が100人いて、治療をしないで放置した場合、その疾患による影響は何もないので、疾患による望ましくないアウトカムは何も起きません。この場合の期待効用U(D–A–)は1で最大です。これは疾患確率P(D+)が0の場合に相当します。これらの二つの場合の中間で、100人中50人がその疾患に罹患している場合を考えてみましょう。治療をしないで、放置した場合、100人中50人には、疾患による望ましくないアウトカムが起き、U(D–A–)とU(D+A–)の差の半分だけ期待効用の値は小さくなります。これは疾患確率P(D+)が0.5の場合に相当します。
これらをグラフで示すと、右下のグラフの様になります。横軸が疾患確率P(D+)、縦軸が効用値U(A–)です。どちらの軸も0~1の範囲の値です。
P(D+)=0の場合、U(A–)=U(D–A–)となります。そして、P(D+)=1の場合、U(A–)=U(D+A–)となります。これらの2点を直線で結ぶと、疾患確率P(D+)と治療しない場合の期待効用U(A–)の関係が示されます。
図1および図2に関係する文献:
Neumann PJ, et al. ed. :Cost-Effectiveness in Health and Medicine. 2nd., 2017.
Pauker SG, Kassirer JP: The threshold approach to clinical decision making. N Engl J Med 1980;302:1109-17. doi: 10.1056/NEJM198005153022003 PMID: 7366635
Kassirer J, Wong J, Kopelman R: Learning Clinical Reasoning. 2nd Edition. 2010, Wolters Kluber, Lippincott, Williams & Wilkins, PA, USA.
Sox HC, Higgins M, Owens DK: Medical Decision Making (2nd ed.). 2013, Wiley-Blackwell.
Straus SE, Glasziou P, Richardson WS, Haynes RB: Evidence-Based Medicine: How to practice and teach EBM. (5th edition) . 2019, Elsevier, London, UK. 第5版

図2は、治療する場合の期待効用U(A+)と疾患確率P(D+)の関係を決定木を用いて解析するためのものです。治療しない場合と同様に、疾患確率P(D+)の一次関数linear functionでU(A+)が計算され、両者の関係は、傾きがU(D+A+)とU(D–A+)の差、U(D–A+)を切片とする直線で表されます。
U(D–A+)は疾患でないのに治療を受けることによる、害、負担、費用により決まります。これらにより、疾患に罹患していないにもかかわらず、効用値が低下します。
U(D+A+)は疾患があって、治療を受けることにより改善した期待効用値の値になります。

治療閾値Therapeutic thresholdとは、Kassirer J 2010のFigure 4.9の解説から引用すると: “疾患確率を0から1まで水平線で表している。治療閾値は、ある病気の可能性と、利用可能な治療法の益とリスクに関するデータから算出される。この閾値は、治療の基準(ベンチマーク)となるものである。閾値より低い疾患確率では治療を控え、閾値より高い疾患確率では治療が行われる。疾患確率をさらに評価するための追加検査がないことが前提である。そのような検査がない場合、この閾値が適用される。”
“治療閾値Rxは、疾患確率の推定値が、その値より小さければ、治療を控え、大きければ治療を行う値である。治療閾値はその治療法の益とリスクを記述しているデータから計算される”(Pauker SG 1980)。
Kassirer Jはリスクrisksという言葉を用いていますが、Sox HCらは害Harmという言葉を用いています。さらに、Sox HCらは単なる害ではなく、net harm すなわち正味の害と述べています。その意味するところは、疾患確率が1でない場合は、疾患でない者が1 – P(D+)の確率で含まれ、これらの人は本当は疾患ではないのに、治療を受けることになり、その治療によってもたらされる効果はすべてその治療の害として取り扱うということです。間違って、その治療を受けた場合、もし、その治療を受けない場合と比べて、望ましいことがもたらされた場合は、それは引き算した正味の害を用いるということです。しかし、ほとんどの場合、疾患がない場合に不必要な治療を受けることによる益はほとんど無いと言えるでしょう。
ここでは、コストという意味でCを用いています。治療を受けることでもたらされるすべての望ましくないアウトカムに置く価値の大きさとも言えますし、治療の望ましくないすべての効果に置く価値の大きさとも言えます。Kassirer JのリスクやSox HCのHarmと同じ意味です。
治療閾値は:
①疾患確率がその値を超えると治療をした場合の期待効用が治療をしない場合の期待効用を上回るので治療が行われる。
②その疾患に対するその治療法の属性であり、ベンチマークである。
③その治療法の益とコスト(害、負担、費用)から計算される。治療閾値Rx=C/(C+B)=1/(1+B/C)
C=U(D–A–) – U(D–A+) B=U(D+A+) – U(D+A–)
④疾患確率をさらに評価する追加検査が無いことが前提である。
これらについて解説します。
①は当たり前ですね。すでに解説したように疾患確率と治療しない場合あるいは治療した場合の効用値は直線関係にあります。傾きが異なれば、どこかで、交差し、その左右では、どちらかの、つまり、治療しない場合か治療する場合の効用値の方がより大きくなります。なお、横軸が疾患確率で縦軸が効用値で、いずれも0~1の範囲です。
さて、②について考えてみましょう。治療閾値は、治療法の属性で、治療閾値が小さければコストが小さく、益が大きいことを示し、治療閾値が大きければ、コストが大きく、益が小さいこと示します。これは、③の計算式からわかります。
③については、どうでしょうか。Rx=1/(1+B/C)の式から、益と害の比によって治療閾値が決まることが分かります。比ですから、益と害の絶対的な大きさや、益と害の差が異なっていても、比であるB/Cが同じなら同じ治療閾値になります。例えば、B=0.5, C=0.2でもB=0.1, C=0.04でも治療閾値は0.2/(0.2+0.5)=0.04/(0.04+0.1)=0.28となります。この点はよく考える必要があります。正味の益を益から害を引き算した値で求めた場合、つまり正味の益net benefit=B-Cで計算すると、同じ治療閾値でも正味の益が大きい場合と小さい場合があるということになります。今の例でいうと、前者の正味の益0.3、後者の正味の益0.06で前者の方が明らかに大きくなります。正味の益の大きさが、治療開始すべきかどうかの決断に影響を与えるかどうかよく考える必要があります。
また、④も非常に重要です。もし、診断能が高い、すなわち感度・特異度の高い検査を施行して、陰性の結果が出た場合、疾患確率が低下し、治療閾値を下回ることが起き得ます。複数の診断法を実施する場合は、結果がどのような組み合わせになるか、Sox HC 2013の記述を引用すると、”gamble”です。検査結果が陰性で、疾患確率が低下した場合でも、治療閾値を超えていることを確認する必要があると思うのは正しい考え方です。それは、診断法の治療検査閾値Test-treatment thresholdによって知ることができます。これについては、後述する予定です。
実際の診療では、疾患確率が治療閾値を超えても、疾患でない割合、すなわち、1-P(D+)がどれくらいあるのかは、臨床決断に大きく影響します。患者の立場で、考えると、たとえ疾患確率が治療閾値を超えたとしても、本当はその疾患ではないのに、まちがって治療を受ける確率がどれくらいなら許容できるか考えさせてほしいということになるでしょう。Shared Decision Making 協働意思決定で疾患確率も議論の対象にせざるを得ない状況があると考えられます。
図3に関係する文献:
Kassirer J, Wong J, Kopelman R: Learning Clinical Reasoning. 2nd Edition. 2010, Wolters Kluwer, Lippincott, Williams & Wilkins, PA, USA.
Pauker SG, Kassirer JP: Therapeutic decision making: a cost-benefit analysis. N Engl J Med 1975;293:229-34. doi: 10.1056/NEJM197507312930505 PMID: 1143303
Sox HC, Higgins M, Owens DK: Medical Decision Making (2nd ed.). 2013, Wiley-Blackwell.