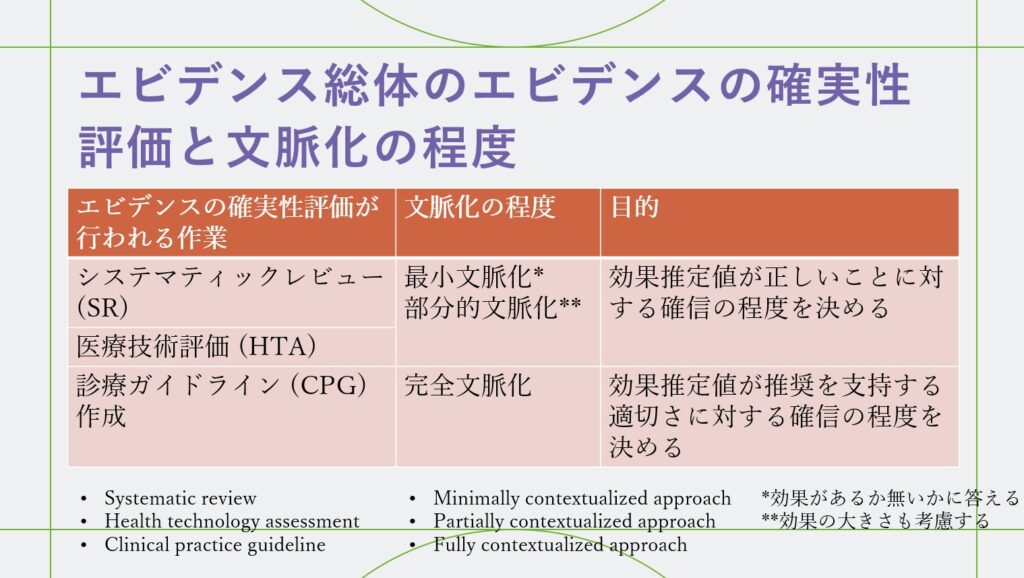
GRADEアプローチにおけるアウトカムごとのエビデンス総体のエビデンスの確実性の評価方法は、システマティックレビュー(SR)、医療技術評価(HTA)と診療ガイドライン(CPG)作成では、異なります。前2者は最小文脈化アプローチMinimally contextualized appproach、または、部分的文脈化のアプローチPartially contextualized approachを用い、CPGでは完全文脈化のアプローチFully contextualized approachを用います。最小文脈化、部分的文脈化のアプローチでは効果推定値が正しいことに対する確信の程度を決めること、完全文脈化では、各アウトカムに対する介入の効果推定値が推奨を支持する適切さに対する確信の程度を決めることが目的です(表1)。
エビデンスの確実性とは:GRADEはエビデンスの確実性を、真の効果が特定の閾値の片側あるいは効果量の選択された範囲にある確実性と定義した」(Schünemann HJ 2022)、あるいは、「GRADEワーキンググループは、個々のアウトカムに対するエビデンスの確実性をレーティングするとき、真の効果が特定の範囲にある、または、ある閾値の片側にあることに、我々がどれくらい確かだと思うかを我々はレーティングしているということを明確にしている」(Hultcrantz M 2017)とされています。
文脈化の程度と他のアウトカムの関連、大・中・小の閾値の設定、正味の益の算出、アウトカムの重要度(価値)の設定、確実性のレーティングの標的の関係を表2に示します。

GRADEワーキンググループ(WG)は2017年にエビデンスの確実性の概念(costruct)について論文(Hultcrantz M 2017)を発表しました。その後のWGの議論を踏まえて、2021年の論文(Zeng L 2021)では、エビデンスの確実性評価の実際的なガイダンスについて述べています。そのガイダンスでは、エビデンスの確実性の評価者は、エビデンスの確実性の概念の何を評価するのかを明確にする必要があると述べており、それを確実性のレーティングの標的(the target of their certainty rating)と呼んでいます。
そして、確実性のレーティングの標的は、エビデンスの確実性評価の文脈化の程度によって異なり、最小文脈化のアプローチでは無効果あるいは効果ありの確実性、または、効果推定値が無効果を含むある範囲にある確実性が標的になります。部分的文脈化のアプローチでは閾値の片側にある確実性あるいは信頼区間が大・中・小の臨床的意味のある閾値と交差する数が標的になります。完全文脈化ではさらに、正味の益を明確にしたうえで、信頼区間の上限値、下限値でそれが反転するかどうかを見る(Hultcrantz M 2017)、あるいは、望ましくない効果の上限値の総和への影響を見る(Schünemann HJ 2022)ことになります。
完全文脈化のアプローチを用いる場合、前作業として部分的文脈化のアプローチによる各アウトカムに対する効果推定値の確実性の評価を行うことが勧められています。
大・中・小の閾値を設定する際には、絶対効果を用い、アウトカムの重要度を反映する必要があります。閾値はリスク差×アウトカムの重要度(効用値)をスケールとして用います。

効果推定値の95%信頼区間がこれら閾値といくつ交差するかによって、エビデンスの確実性をレートダウンします。1つの閾値と交差する場合は、1レベルレートダウン;2つの閾値と交差する場合は、2レベルレートダウン;3つの閾値と交差する場合は、3レベルレートダウンが原則です。

効果推定値が大の閾値を超えるようなありそうもない大きな効果を示している場合、あるいは、わずかまたは小さな効果の場合に、Review Information Size(RIS)レビュー情報量を計算する必要があります。大・中・小の閾値に対する必要なRIS、すなわちその大きさの効果を証明に必要なサンプルサイズを計算し、その結果で、実際のサンプルサイズが•大きな効果の閾値より少ない ⇒ 3レベルレートダウン;•中等度の効果の閾値より少ない ⇒ 2レベルレートダウン;•小さな効果の閾値より少ない ⇒ 1レベルレートダウンすることが提案されています。ただし、効果推定値の95%信頼区間の大・中・小の閾値との交差と合わせて慎重に判断する必要があります。
OISは臨床的に意味のある効果推定値を証明するのに必要なサンプルサイズ。エビデンスの確実性の評価で、部分的文脈化あるいは完全文脈化アプローチを用いる場合は、大・中・小の閾値を設定する必要があり、それぞれに対する必要なサンプルサイズを計算するので、RISという用語を用いる。OIS: Optimal Information Size最適情報量; RIS: Review Information Sizeレビュー情報量
閾値の設定は困難な課題ですが、次のような情報を根拠とすることが提案されています:
•効用値と絶対効果から閾値を設定している研究を参照する。
•効用値に関する研究を参照する。
•閾値が用いられた診療ガイドラインを参照する。
•疾患専門家や意思決定に関与する利害関係者が何らかの情報(経験、文献情報)に基づいて、効用値を考えながら閾値を設定する。
また閾値を設定は、まずアウトカムの重要度を設定し、その後に行うべきとされています。以下の点に留意する必要があります:
•アウトカムの重要度をエビデンス評価の前に決めておく。
•アウトカムの重要度を決めてから閾値を設定する。
•アウトカムの重要度に関する新知見が得られたら閾値をアップデートする。
•アウトカムの重要度は少なくとも疾患に特異的であり、相対的な値なので、同じアウトカムがどのような疾患でも同じ価値を持つわけではない。また、介入により取り扱うべきアウトカムが異なることもあるので、同じ疾患でも、他のアウトカムの構成によって同じアウトカムでも異なる値を設定することがありうる。0~100(あるいは0~1.0)の値を設定する。
また連続変数アウトカムの場合の閾値の設定に関しては以下の提案がされています:
•大・中・小の閾値に関する経験的推定値がある場合、それを用いる。例:Chronic Respiratory Questionnaire 7ポイントスケールの場合、0.5, 1.0, 1.5; Visual Analogue Scaleの場合6, 10, 14
•Minimal Important Difference (MID)の推定値が得られる場合、それを小さい効果の閾値として用いる。
•標準化平均値差(SMD)を用いて、SMD 0.2, 0.5, 0.8に閾値を設定する。
•何らかの情報に基づく専門家の推定値。
#################################
Hultcrantz M 2017で述べられていた完全文脈化のアプローチのステップは以下の様になります:
1.絶対効果の大きさとアウトカムの重要性の積の総和として正味の益を計算する(Alper BS 2019)。
2.各アウトカムに対する絶対効果の上限値と下限値で正味の益が逆転するかを見る。(逆転の閾値は0または評価者が設定した値)。
3.逆転する場合は、そのアウトカムに対する効果の不精確性をレートダウンし、(他のエビデンスの確実性評価ドメインと合わせて)エビデンス総体のエビデンスの確実性をレートダウンする。
なお、連続変数アウトカムの場合はそのままでは正味の益の計算に含めることはできません。
#################################
Schünemann HJ 2022の論文で述べられている完全文脈化のアプローチのステップは以下の様になります:
0. 部分的文脈化アプローチで各アウトカムに対する効果推定値の不精確性の評価を行う。
1.益のアウトカムに対する効果推定値の95%信頼区間下限値に基づいてありうる最小の望ましい絶対効果量を特定する。
2.害のアウトカムに対する効果推定値の95%信頼区間上限値に基づいてありうる最大の望ましくない絶対効果量を特定する。
3.最小の望ましい効果を集約(aggregate)し、それに基づいて介入を推奨するのに許容しうる最大のありうる望ましくない効果の総和(overall)を決める(必要に応じて費用なども考慮する)。個々の望ましくないアウトカムに対する効果のありうる最大値に基づいて不精確性のレーティングを変更する必要があるかを決めるのにこの総和の閾値を考慮する。複数の望ましくない効果がある場合、これを各アウトカムについて個別に、あるいは集積した上で、行わなければならないことに留意する。
4.望ましくない効果の信頼区間が、許容しうる最大のありうる望ましくない効果の閾値と重なるかどうかを判定する。もし「はい」なら、完全文脈化アプローチの精確性のレーティングは変更されない。益と害のバランスが確実でないかもしれない、すなわち、明確な正味の望ましい健康効果がないため、ガイドライン委員会は通常、条件付推奨とする。
5.閾値が交差しない場合、不精確性に基づく不確実性は決定に影響を与えない可能性があり、正味の望ましい効果があるため、望ましい効果と望ましくない効果に対する不精確性の確実性を下げることは、推奨や決断のために必要ないであろう(これはまれであろう)。そして、総体のエビデンスの確実性が全体として中または高い場合、ガイドライン委員会は多くの場合、強い推奨とする。エビデンス全体の確実性が非常に低いか低い場合、たとえ正味で望ましい効果があったとしても、ガイドライン・パネルは通常、条件付き推奨とする。
注)例を挙げていないが、仮に、部分的に文脈化されたアプローチを用いて、どのアウトカムも不精確性で格下げが行われなかったとしても、すべての望ましいアウトカムまたはすべての望ましくないアウトカムの不確実性の累積が、望ましいアウトカムまたは望ましくないアウトカムの累積効果を不精確にする可能性がある。すべての望ましい結果または望ましくない結果を組み合わせた後の累積不確実性が非常に大きく、信頼区間が閾値を超えるような場合には、1つまたは複数の主要なアウトカムの不精確性を理由とした格下げが正当化される可能性がある。
なお、同論文には部分的文脈化のアプローチのステップも記述されていますので、必要に応じて、参照してください。
#####################################
完全文脈化のアプローチは複雑で、実行も容易とは思えません。各アウトカムに対する効果推定値の95%信頼区間の幅を評価する際に、大・中・小の区切りを閾値として設定するだけの様にも見えますし、大・中・小の閾値の設定はアウトカムの重要度の設定と同じように、個人によって差が出てくるように思えます。また、もともと絶対効果が小さい、あるいは、重要度が低いアウトカムに対する効果推定値の不確実性は、意思決定あるいは推奨に影響しない可能性が高く、エビデンスの確実性の厳密な評価をする意義が低くなると思います。
文献:
Hultcrantz M, et al: The GRADE Working Group clarifies the construct of certainty of evidence. J Clin Epidemiol 2017;87:4-13. doi: 10.1016/j.jclinepi.2017.05.006 PMID: 28529184
Alper BS, et al: Defining certainty of net benefit: a GRADE concept paper. BMJ Open 2019;9:e027445. doi: 10.1007/s11882-011-0185-8 PMID: 31167868
Zeng L, et al: GRADE guidelines 32: GRADE offers guidance on choosing targets of GRADE certainty of evidence ratings. J Clin Epidemiol 2021;137:163-175. doi: 10.1016/j.jclinepi.2021.03.026 PMID: 33857619
Schünemann HJ, et al: GRADE guidance 35: update on rating imprecision for assessing contextualized certainty of evidence and making decisions. J Clin Epidemiol 2022;150:225-242. doi: 10.1016/j.jclinepi.2022.07.015 PMID: 35934266






