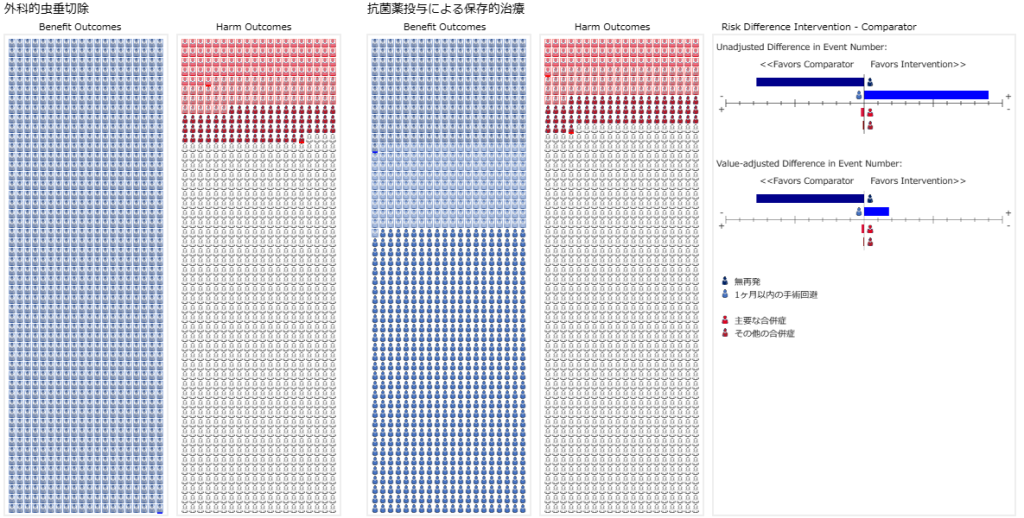
介入の効果は対照群と比較した相対的効果指標であるリスク比Risk Ratio (RR)、オッズ比Odds Ratio (OR)、生存分析の場合はハザード比Hazard Ratio (HR)で評価されることが一般的です。Risk Difference (RD)をメタアナリシスで統合することももちろんできますが、これらの効果指標が用いられることが多く、エビデンス総体の非一貫性の評価の際はRRまたはHRを用いることが望ましいとされています。ネットワークメタアナリシスではORが用いられることが多いようです。まずこれらの効果指標がどのように計算されるかを見ておきましょう。

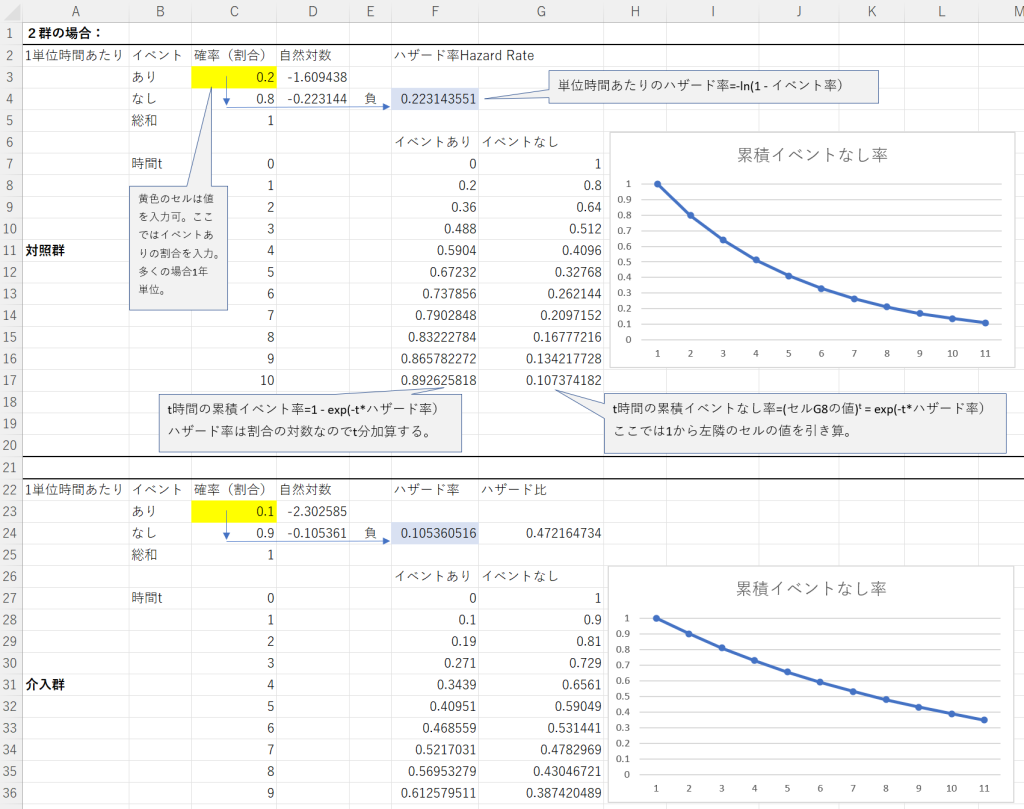
一方、望ましい効果(益)の大きさ、望ましくない効果(害)の大きさを異なるアウトカム間で比較するには、絶対効果を示すリスク差Risk Difference (RD)を用いる必要があります。RR, OR, HRでは同じ値であってもベースラインリスクが異なるとRDが異なるので、絶対効果の大きさは同じとはならず、そのまま比較することはできないことは明らかです。一方、RDは値が2倍になれば、2倍の人数の人が影響を受けることは明確です。
メタアナリシスでOR、RRあるいはHRを統合した場合、それらについて、エビデンスの確実性の評価をランダム化比較試験であれば、バイアスリスク、非直接性、不精確性、非一貫性、出版バイアスの5ドメインから評価します。その先、望ましい効果(益)、望ましくない効果(害)の大きさと、益と害のバランス=正味の益を評価するためには、絶対効果=RDを求める必要があります。そのため、GRADEアプローチではSummary-of-Findings (SoF)table結果のまとめ表では①相対効果指標と95%信頼区間、②対照群の絶対リスク、③介入群の絶対リスク、and/or、④絶対効果と95%信頼区間を記述することが求められています。相対効果指標と95%信頼区間はメタアナリシスから得られます。対照群の絶対リスクはメタアナリシスに含めた研究の対照群の総症例数から算出した値、疾患レジストリなど他のデータソースからの値、想定される高・中・低リスクの値を設定するなどが考えられます。
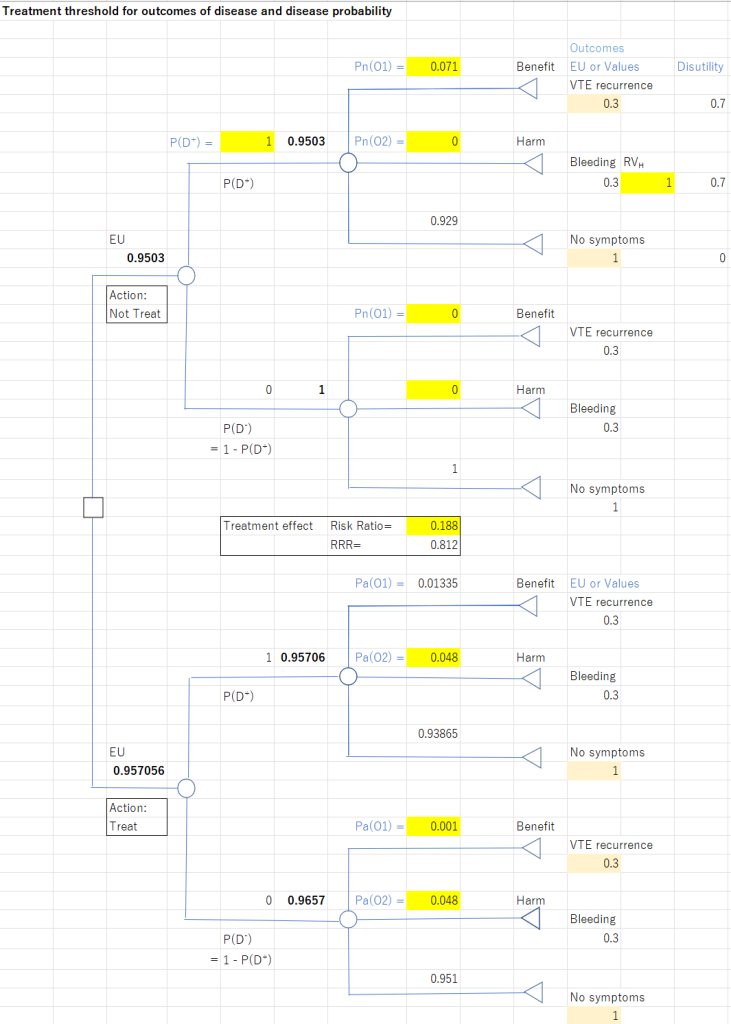
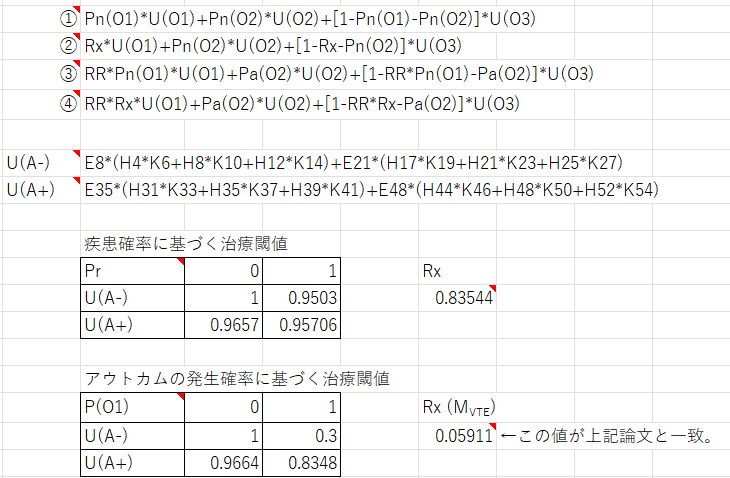
絶対効果はRR、OR、HRと対照群の絶対リスク=CER (Comparator Event Rate)から以下に示す方法で計算することができます。

ORからRRを計算する方法は図4に、HRからRRを計算する方法は図5に示す通りです。数式の形を変えるだけなので、単なる数学的な課題で、だれが考えても同じになります。
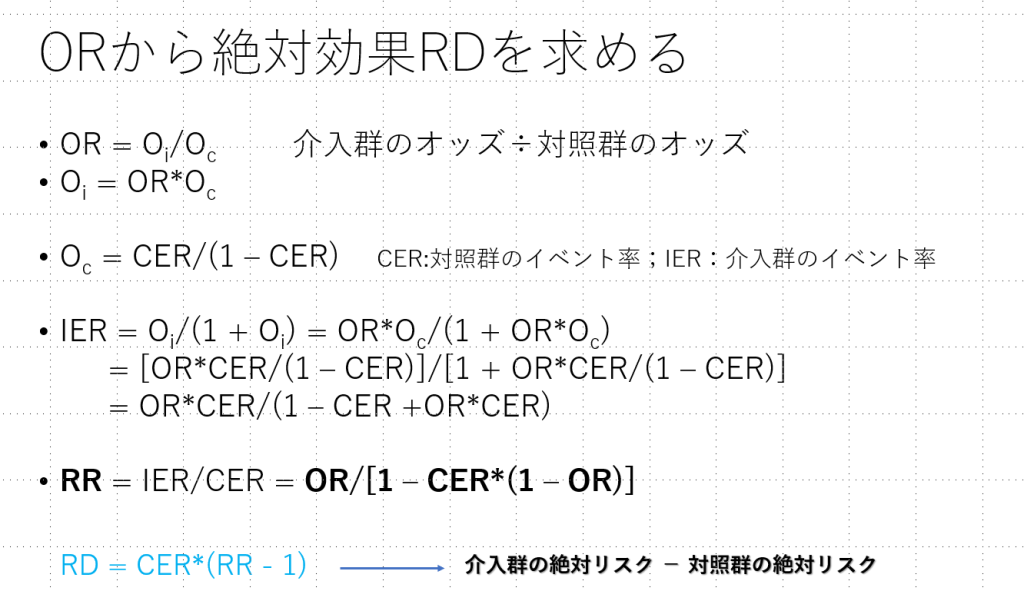

RDを計算する際に、介入群の絶対リスク-対照群の絶対リスクを計算する方が分かりやすいと思います。図4と図5、6は逆になっていますが、測定されるアウトカムが有害事象なのか有益事象なのかによってもどちらが分かりやすいかはまた変わってきます。
いろいろな考え方がありえますが、正味の益=益の大きさ-害の大きさで計算し、プラスの値であれば、正味の益が大きく、マイナスの値であれば正味の害が大きいというようにするためには、益のアウトカムには有益事象を測定し、害のアウトカムには有害事象を測定し、介入群の絶対リスク-対照群の絶対リスクを計算すると介入群の益が大きければ益はプラスの値、介入群の害が小さいと害はマイナスの値になり、正味の益=益の大きさ-害の大きさの計算ではプラスの値からマイナスの値を引き算するので、全体としてプラスが大きくなります。もし、介入群の害が対照群より大きい場合は、害はプラスの値になり、正味の益はその分引き算されて小さくなります。このような取り扱いが分かりやすいのではないかと思います。
アウトカムが有害事象か有益事象かに合わせてプラスマイナスを変えて計算し、RD=CER×(1-RR)ですべて計算する方法もあり得ます。その方が分かりやすい人もいると思います。また、グラフ化する際にはもう少し考慮すべき点がありますが、皆さんも考えてみて下さい。
そして、100人あたり、1000人あたり、10000人あたりの頻度人数にするには、RDにこれらの値を掛け算することになり、四捨五入するか切り捨てるかも決めておく必要があるでしょう。