バイアスの効果はリスク比あるいはオッズ比などで表すことができます。バイアスの効果を定量的に推定できるのであれば、実際に得られた効果推定値をそれで調整して真の値により近づけることができます。
バイアスのモデル化についてはTurner RM 2009らのJournal of the Royal Statistical Society Series Aに発表された論文が精細な内容で参考になります。個別研究のバイアスドメイン・項目を評価しバイス調整をしたうえで、複数の研究のメタアナリシスの統合値を得る手法です。
バイアスの効果とバイアス調整について図にしてみました。
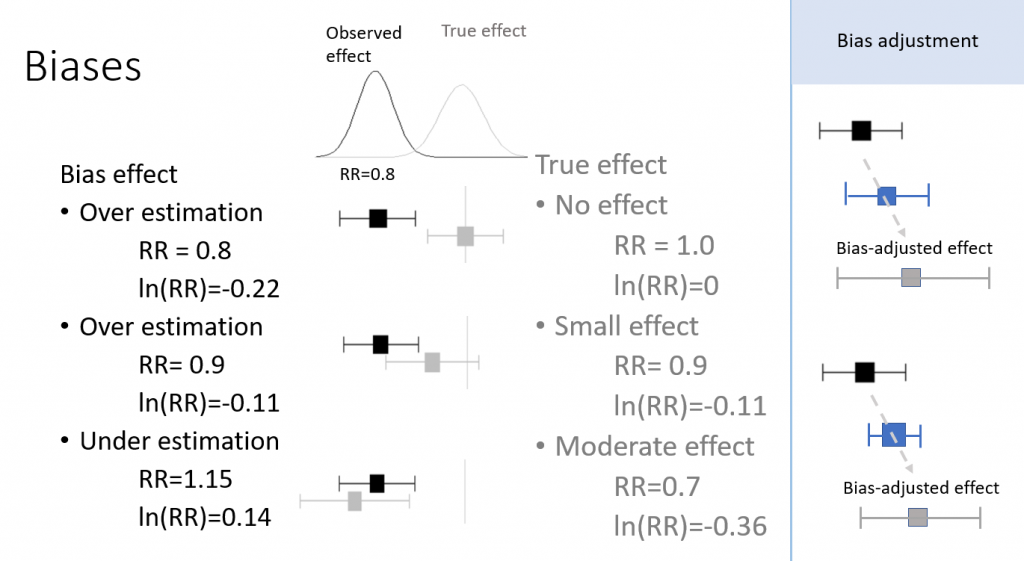
バイアスの効果には大きさと方向(過大評価、過小評価)と不確実性の3つの要素があります。
バイアスの効果を定量的解析する場合には、例えば、リスク比あるいはオッズ比を効果指標にした場合、自然対数に変換すると、正規分布に従うとみなせ、研究で得られた効果推定値は真の値とバイアス効果の加算された値になります。バイアス調整をする場合は、推定されるバイアス効果の大きさをリスク比で表し、その自然対数を引き算することで、真の値が得られはずです。分散は両者の合計になります。多変量正規分布の原理です。
メタアナリシスで得られた統合値の95%信頼区間の上限値(あるいは下限値)がNull effectあるいは臨床的閾値を超えるほどの大きさのバイアスの効果は簡単に計算できます。一般的に行われているバイアスリスクRisk of biasの評価結果でバイアスリスクが高く、バイアスの大きさがこの値よりも大きな効果を持っていると判断できる場合は、エビデンスの確実性が低くなると考えることができます。もし、そのようなバイアス効果の大きさがあり得ないほど大きいのであれば、ある程度のバイアスリスクがあっても、エビデンスの確実性は高いと考えることができるでしょう。
文献:
Turner RM, Spiegelhalter DJ, Smith GC, Thompson SG: Bias modelling in evidence synthesis. J R Stat Soc Ser A Stat Soc 2009;172:21-47. PMID: 19381328
Turner RM, Lloyd-Jones M, Anumba DO, Smith GC, Spiegelhalter DJ, Squires H, Stevens JW, Sweeting MJ, Urbaniak SJ, Webster R, Thompson SG: Routine antenatal anti-D prophylaxis in women who are Rh(D) negative: meta-analyses adjusted for differences in study design and quality. PLoS One 2012;7:e30711. PMID: 22319580
Darvishian M, Gefenaite G, Turner RM, Pechlivanoglou P, Van der Hoek W, Van den Heuvel ER, Hak E: After adjusting for bias in meta-analysis seasonal influenza vaccine remains effective in community-dwelling elderly. J Clin Epidemiol 2014;67:734-44. PMID: 24768004
Dias S, Sutton AJ, Welton NJ, Ades AE: Evidence synthesis for decision making 3: heterogeneity–subgroups, meta-regression, bias, and bias-adjustment. Med Decis Making 2013;33:618-40. PMID: 23804507
Thompson S, Ekelund U, Jebb S, Lindroos AK, Mander A, Sharp S, Turner R, Wilks D: A proposed method of bias adjustment for meta-analyses of published observational studies. Int J Epidemiol 2011;40:765-77. PMID: 21186183
Wilks DC, Mander AP, Jebb SA, Thompson SG, Sharp SJ, Turner RM, Lindroos AK: Dietary energy density and adiposity: employing bias adjustments in a meta-analysis of prospective studies. BMC Public Health 2011;11:48. PMID: 21255448
Wilks DC, Sharp SJ, Ekelund U, Thompson SG, Mander AP, Turner RM, Jebb SA, Lindroos AK: Objectively measured physical activity and fat mass in children: a bias-adjusted meta-analysis of prospective studies. PLoS One 2011;6:e17205. PMID: 21383837
Schnell-Inderst P, Iglesias CP, Arvandi M, Ciani O, Matteucci Gothe R, Peters J, Blom AW, Taylor RS, Siebert U: A bias-adjusted evidence synthesis of RCT and observational data: the case of total hip replacement. Health Econ 2017;26 Suppl 1:46-69. PMID: 28139089
Doi SA, Barendregt JJ, Onitilo AA: Methods for the bias adjustment of meta-analyses of published observational studies. J Eval Clin Pract 2013;19:653-7. PMID: 22845171
McCarron CE, Pullenayegum EM, Thabane L, Goeree R, Tarride JE: Bayesian hierarchical models combining different study types and adjusting for covariate imbalances: a simulation study to assess model performance. PLoS One 2011;6:e25635. PMID: 22016772
McCarron CE, Pullenayegum EM, Thabane L, Goeree R, Tarride JE: The importance of adjusting for potential confounders in Bayesian hierarchical models synthesising evidence from randomised and non-randomised studies: an application comparing treatments for abdominal aortic aneurysms. BMC Med Res Methodol 2010;10:64. PMID: 20618973
Phillippo DM, Dias S, Welton NJ, Caldwell DM, Taske N, Ades AE: Threshold Analysis as an Alternative to GRADE for Assessing Confidence in Guideline Recommendations Based on Network Meta-analyses. Ann Intern Med 2019;170:538-546. PMID: 30909295
Caldwell DM, Ades AE, Dias S, Watkins S, Li T, Taske N, Naidoo B, Welton NJ: A threshold analysis assessed the credibility of conclusions from network meta-analysis. J Clin Epidemiol 2016;80:68-76. PMID: 27430731
Phillippo DM, Dias S, Ades AE, Didelez V, Welton NJ: Sensitivity of treatment recommendations to bias in network meta-analysis. J R Stat Soc Ser A Stat Soc 2018;181:843-867. PMID: 30449954

