バイアスとは
バイアスは「研究結果の系統的な偏り、あるいは、推定の真実からの系統的な偏り」と定義されています。系統的とは? 偶然による偏りに対して、偶然起きる偏りではないので、系統的な偏りと言います。系統的systematic vs 偶然random という考え方をしているということです。偶然による偏りは、統計学的に説明可能でサンプルサイズが小さいほど大きくなります。バイアスによる偏りは経験的empiricalなデータは限られており、バイアス効果の大きさと方向(過大評価か過小評価か)については評価者が推定せざるをえないことがほとんどです。
実際に得られた結果の効果推定値および信頼区間Confidence intervalから、偶然による偏りだけなのか、バイアスによる偏りなのか、両方が混ざっているのかを見分けるのは難しいです。なお、頻度論派Frequentistの95%信頼区間は同じことを繰り返したら95%の場合はその範囲に本当の値が含まれるということを意味しています。5%の場合は、その範囲外になります。ベイジアンBayesianのアプローチであれば、95%確信区間Credicble intervalは真の値を95%の確率で含む範囲です。
さて、バイアスは多数存在しますが、バイアスの原因となる要素がその研究にあるかどうかを判断することは可能です。それがその研究にあれば、その結果あるいは効果推定値はバイアスのため、偏っている可能性が高くなります。そのようなアプローチが必要になります。
真の値を推定することは、もしバイアス効果の大きさが推定できれば、それによって調整することで、可能になります(Quantitative bias analysis)。例えば、得られた結果のリスク比RR=0.8で、バイアスの効果がRR=0.9であれば、真の効果推定値はRR = 0.8/0.9 = 0.89 =exp[ln(0.8)-ln(0.9)] = exp[-0.223-(-0.105)] = exp(-0.118)です。結果RRの分散とバイアス効果のRRの分散を合計するとバイアスで調整した真の効果の推定値の分散はそれらの合計になります。バイアス効果のRRの分散はレビュアが推定値を設定する必要があります(Turner RM 2009)。*ln 自然対数;exp Exponential (Excelの関数の表示ln(), exp()と同じです, なお、Rでは自然対数はlog())。
また、バイアスの効果の大きさがどれ位あれば望ましい結果が望ましくない結果に反転するかも知ることができます(Bias adjustment thresholds analysis)(Phillippo DM 2018)。しかしながら、そこまで分析を行うケースは少なく、Cochrane risk of bias toolのように、大きなバイアス(あるいは”実質的なバイアス” material bias)のリスク=可能性がどれくらいあるかを評価することが一般的です。
バイアスは交絡バイアス、選択バイアス、情報バイアスの3つに分類されるのが一般的です(Lash TL 2021)。
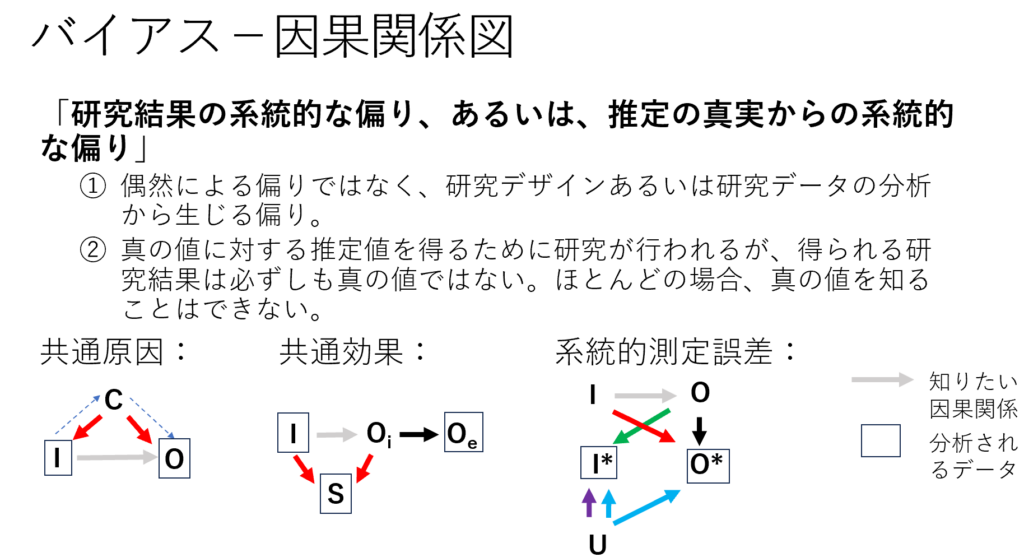
矢印の始点の方が原因で終点の方が結果を示します。IはIntervention介入またはEと書いてExposure要因暴露、CはCommon cause共通原因=Confounder交絡因子、OはOutcomeアウトカムを表します。OiはIntermediate outcome中間アウトカム、OeはEndpointエンドポイントです。I*は測定された介入、O*は測定されたアウトカムを表します。Uは測定誤差を引き起こす因子で、多くの場合不明です。
共通原因は交絡バイアス、共通効果は選択バイアス、系統的測定誤差は情報バイアスに対応します。
I←C→O; I→S→Oi←Oeと記述しても共通原因、共通効果であるこをと表現できます。
バイアスの効果を分析する際に、有向非巡回グラフDirected Acyclic Graph (DAG)が用いられることがあります。DAGは因果関係図Causal Diagramと呼ばれることもあります。それぞれの変数がバイアスになりうるかを検討するのに有力なツールです。図には、Luijendijk HJ 2020の論文に基づいて、汎用性のあるDAGの3つのバイアスのタイプについて示してあります。
共通効果→選択バイアス
バイアスの議論の際に、よく引用されるBerkson’s biasは選択バイアスとして知られていますが、共通効果のDAGを使って説明されます(Westreich D 2012)。例えば、クリニック受診患者を対象として糖尿病と認知症の関係を分析した場合、受診の原因が糖尿病の場合もあり認知症の場合もあります。クリニック受診が共通効果になります。クリニックを受診しない患者は選択せず、クリニック受診患者だけを選択して糖尿病と認知症の関係を分析するとバイアスが生じます。このようなバイアスは、前向き研究でも後ろ向き研究でも、観察研究でもランダム化比較試験でも起きる可能性があります。
共通効果で条件付けされるすなわちconditioned on (分類される)ある層だけを対象として選択したり、共通効果で調整するとバイアスが生じます。すなわち、図に示す変数Sに基づく層のひとつを分析する、あるいは変数SでIとOeの関係を調整した分析を行うとバイアスが生じます。このようなバイアスの結果は過大評価になる場合も、過小評価になる場合もあり、例えば、上記の例だと糖尿病は認知症のリスクを高めることはないという結果が得られる可能性があります。
SがOiの影響をうけて変動する結果生じるバイアスとして、脱落によるバイアス、症例減少バイアスAttrition biasがあります。その場合、介入群の方で脱落がより多いというような、Iからの影響も受けます。
コンシールメントがないためにランダム化が歪んで起きるバイアスも共通効果で説明できるはずです。皆さんも考えてみて下さい。
共通効果はCollider 合流因子とも呼ばれ、共通効果によるバイアスは選択バイアスに相当します。選択バイアスをCollider biasと呼ぶこともあります。
共通原因→交絡バイアス
共通原因は交絡因子に相当し、介入とアウトカムの両方に関係がある因子です。因果関係はI←C→Oの方向です。共通原因=交絡因子の影響によって介入が変動し、アウトカムも変動する場合に、介入のアウトカムに対する効果を単純に分析すると交絡バイアスが生じます。交絡バイアスは分析の時点で層別分析や多変量回帰分析などで調整することが可能ですが調整の程度はさまざまです。
例えば、盲検化がされていないため“別の治療を受ける”という“治療企図からの乖離”が起きると、対象者の介入の内容を変え、治療の効果=アウトカムを変えてしまうので、交絡因子になります。共通原因により生じるバイアスは交絡バイアスに相当します。
系統的測定誤差→情報バイアス
系統的測定誤差あるいは誤分類はさまざまな原因で起きます。図に示すUは、未知の因子ですが、それが影響して測定誤差が生じた介入がI*、アウトカムがO*です。測定誤差の原因がIにある場合も(赤い矢印)、Oにある場合も(緑の矢印)あります。
例えば、盲検化がされていないために、アウトカム測定者が患者が受けている治療を知ることができるため、介入に有利な測定結果を出してしまい、過大評価の結果が得られた場合、系統的測定誤差の赤の矢印の因果関係が作動したための情報バイアスの一例になります。このようなバイアスは介入が新しい治療法でアウトカム測定者がより高い効果を期待しているような場合に起き得ます。このようなバイアスは検出バイアスに相当します。
矢印の始点の方が原因で終点の方が結果を示します。IはIntervention介入またはEと書いてExposure要因暴露、CはCommon cause共通原因=Confounder交絡因子、OはOutcomeアウトカムを表します。OiはIntermediate outcome中間アウトカム、OeはEndpointエンドポイントです。I*は測定された介入、O*は測定されたアウトカムを表します。Uは測定誤差を引き起こす因子で、多くの場合不明です。
DAGの各変数
これら、I, C, O, Oi, Oe, I*, O*, Uは変数を表し、例えば、I=1は介入あり、I=0は介入なし、のような値が設定され、例えばO=1治癒、O=0非治癒とすると、条件付き確率の式を用いてP(O=1|I=1)と記述すると、Iが介入ありの場合のOが治癒となる確率を表し、介入群の治癒確率を表すことになります。
図中ボックスで囲んであるのが実際の分析対象となる変数です。Sは選択を表す変数ですが、Sのボックスの意味は、介入と中間アウトカムに基づく対象者の除外が研究デザインあるいは分析のしかたで起きることを示しています。Sの値が0なら対照、1なら介入という設定や、0は非脱落、1は脱落、0は報告する、1は報告しないというような値を設定できます。
左下の共通原因のDAGの青い点線はI→C→Oという本来ないはずの因果関係がBack door pathバックドア経路として開かれるということを示しています。
系統的測定誤差のDAGは必ずしも矢印のすべてが同時に起きる事象ということではなく、どの矢印が有効かは、分析対象の研究によって異なってきます。
観察研究の場合は、IをE要因曝露に置き換えます。
バイアスは数多く存在し、観察研究はバイアスの影響を受けやすいですが、ランダム化比較試験もバイアスに無縁ではなく、多くのバイアスの影響を受ける可能性があります。
ランダム化比較試験のバイアス評価について、特にCochrane risk of bias tool ver. 2.0 RoB 2)を中心にスライドと解説の資料を作成しました。RoB 2を用いたランダム化比較試験のエビデンス評価の作業をする際に参考にしてください → Link
文献:
Turner RM, Spiegelhalter DJ, Smith GC, Thompson SG: Bias modelling in evidence synthesis. J R Stat Soc Ser A Stat Soc 2009;172:21-47. PMID: 19381328 PubMed
Phillippo DM, Dias S, Ades AE, Didelez V, Welton NJ: Sensitivity of treatment recommendations to bias in network meta-analysis. J R Stat Soc Ser A Stat Soc 2018;181:843-867. PMID: 30449954 PubMed
Lash TL, VanderWeele TJ, Haneuse S, Rothman KJ: Modern Epidemiology (FORTH EDITION). 2021, Wolters Kluwer, PA, USA. Amazon
Luijendijk HJ, Page MJ, Burger H, Koolman X. Assessing risk of bias: a proposal for a unified framework for observational studies and randomized trials. BMC Med Res Methodol. 2020 Sep 23;20(1):237. doi: 10.1186/s12874-020-01115-7. PubMed
Westreich D: Berkson’s bias, selection bias, and missing data. Epidemiology 2012;23:159-64. doi: 10.1097/EDE.0b013e31823b6296 PMID: 22081062 PubMed
Hernán MA, Monge S: Selection bias due to conditioning on a collider. BMJ 2023;381:1135. doi: 10.1097/EDE.0000000000000031 PMID: 37286200 PubMed
バイアスに関する論文はたくさんありますが、役立ちそうな文献を少しあげておきます:
Hernán MA, Monge S: Selection bias due to conditioning on a collider. BMJ 2023;381:1135. doi: 10.1136/bmj.p1135 PMID: 37286200 PubMed
Sjölander A: Selection Bias with Outcome-dependent Sampling. Epidemiology 2023;34:186-191. doi: 10.1097/EDE.0000000000001567 PMID: 36722800 PubMed
Lu H, Cole SR, Howe CJ, Westreich D: Toward a Clearer Definition of Selection Bias When Estimating Causal Effects. Epidemiology 2022;33:699-706. doi: 10.1097/EDE.0000000000001516 PMID: 35700187 PubMed