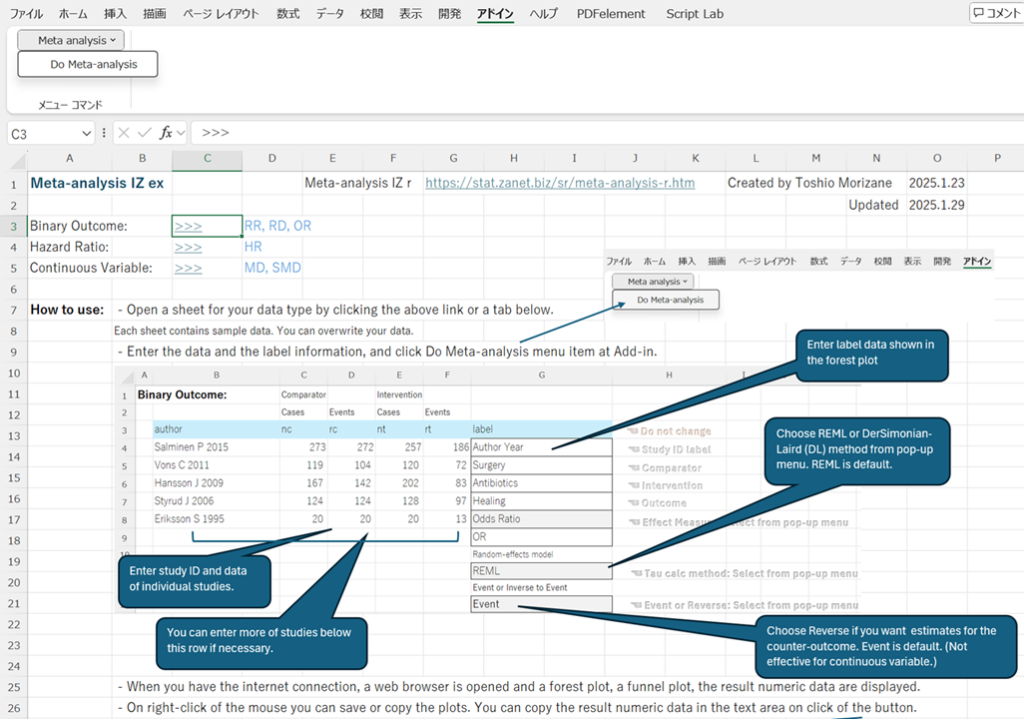
メタアナリシスのためのデータをExcelで用意し、そのファイルをドラグアンドドロップすると、メタアナリシスを実行し、Forest plotとFunnel plotを作成するウェブページを作りました。
解析はJavaScriptで作成したコードで行っており、MathライブラリとjStatライブラリを用いています。インターフェース関連でjQueryも用いています。
メタアナリシスはInverse-variance method分散逆数法、ランダム効果モデルによる方法で、研究間の分散はRestricted Maximum Likelihood (REML)法(Viechtbauer W 2005)を用いています。
ExcelシートはMindsのテンプレートをそのまま用いて、データを入力します。図1は介入研究用(RoB2)の例です。介入、対照、アウトカムの欄にはデータを入力する必要があります。さらに、研究コード、リスク人数と書いてあるデータの部分、そして効果指標のタイプは設定する必要があります。
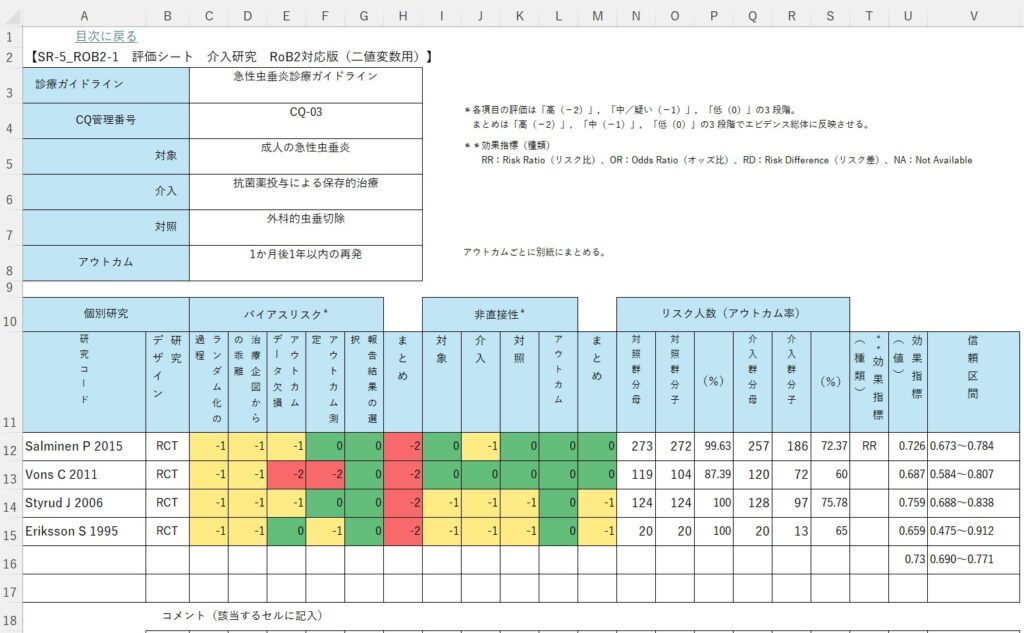
必要なデータを入力したらファイルを保存します。
ブラウザで次のウェブページを開いてください。Meta-analysis IZ mi
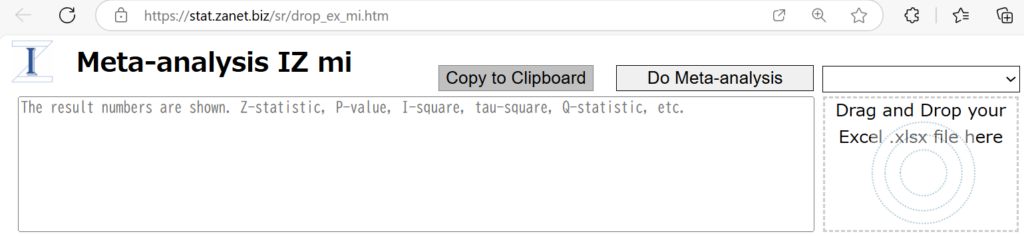
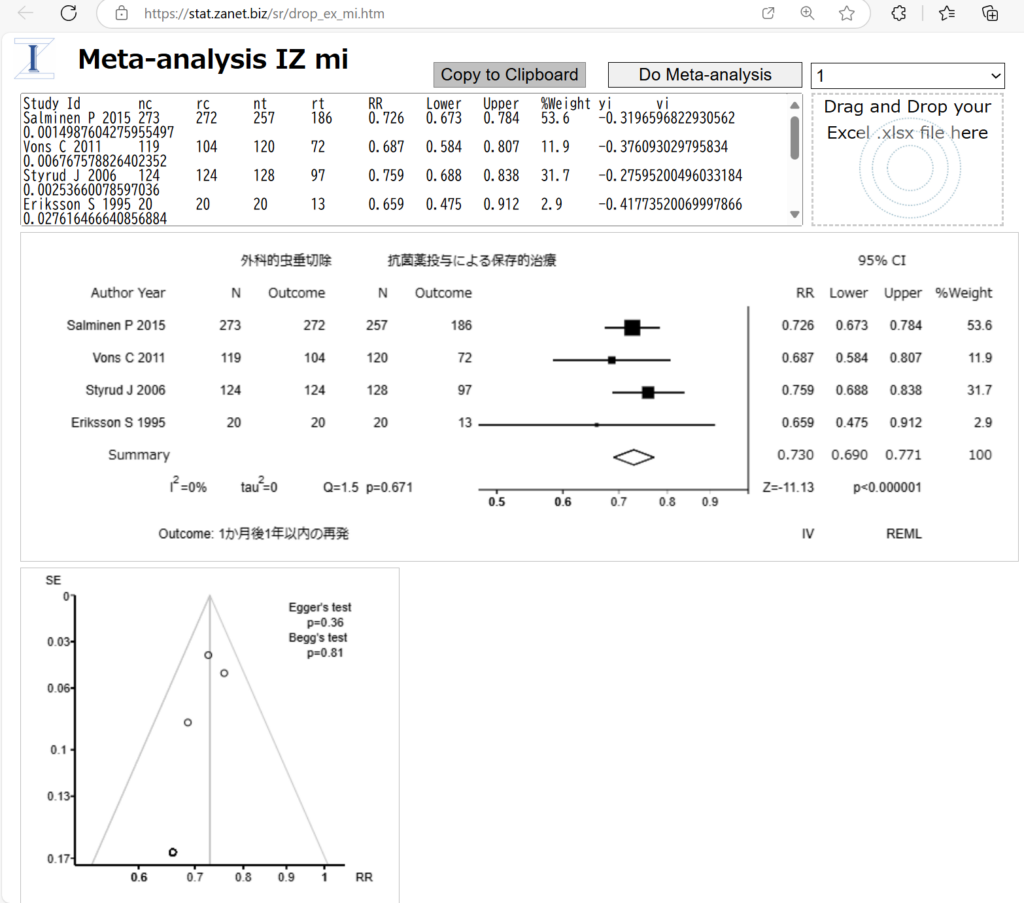
右の円が描かれているエリアにExcelのファイルをドラグアンドドロップすると、すぐ上のドロップダウンメニューにシート名の一覧が表示されるので、メタアナリシスの対象のシートを選択し、その左のDo Meta-analysisのボタンをクリックしてください。Forest plotとFunnel plotが表示されます。また、結果の数値データが上のテキストエリアに書き込まれます。
Do Meta-analysisの実行直後は、各研究の効果指標と95%信頼区間、統合値と95%信頼区間の値がクリップボードに格納されているので、Excelシートの効果指標(値)のセルに貼り付けることができます。図1の例であれば、セルU12を選択して貼り付けます。
Forest plotとFunnel plotは右クリックして保存したり、コピーして貼り付けたりできます。数値データは必要に応じて、Copy to Clipboardボタンをクリックして、クリップボード経由でExcelシートに貼り付けられます。
Meta-analysis IZ miはRoB2用のシートだけでなく、それ以外のシートにも対応しています。効果指標のタイプは、二値変数アウトカムのRR, OR, RD、ハザード比HR、連続変数アウトカムのMD, SMDに対応しています。評価シートの効果指標(種類)でタイプを設定してください。
使用法の解説動画はこちらです (YouTube Link)。
ここで紹介した、Mindsの評価シートに対応しているのが、Meta-analysis IZ miですが、メタアナリシスだけで十分な場合は、別のフォーマットでExcelファイルを用意してMeta-analysis IZ izを使うこともできます。こちらは、REML法とDerSimonian-Laird法の指定ができます。
サンプルデータを入力したMindsの評価シートのファイルとMeta-analysis IZ iz用のサンプルデータを入力したファイルはこちらでダウンロードできます。右クリックして保存してから使用してください。
minds-sample-rob2.xlsx
iz-meta-sample.xlsx
メタアナリシスの際に用いている計算式について詳細を知りたい人は、Deeks J and Higgins JPT 2010を参照してください。この解説の時点では、研究間の分散の計算はDerSimonian-Laird法を用いていますが、最近RevManでもREML法も選択できるようになったようです。McKenzie J, Veroniki AAの解説を参照してください。
文献:
Viechtbauer W: Bias and Efficiency of Meta-Analytic Variance Estimators in the Random-Effects Model. Journal of Educational and Behavioral Statistics
Fall 2005, Vol. 30, No. 3, pp. 261–293. Link
Viechtbauer W氏のR package metafor Link The metafor Package: A Meta-Analysis Package for R. Link
Deeks J and Higgins JPT: Statistical algorithm in Reveiw Manager 5. 2010. Link
McKenzie J, Veroniki AA: Introduction to new random-effects methods in RevMan. Link 解説スライド